Корреляционный анализ. Для вычисления коэффициента корреляции и корреляционного отношения предварительно составляются корреляционные таблицы

Для вычисления коэффициента корреляции и корреляционного отношения предварительно составляются корреляционные таблицы. По характеру таблицы можно ориентировочно судить о наличии или отсутствии корреляционной связи между переменными. Например, по двум приведенным ниже таблицам можно сказать, что в первом случае такая связь может быть обнаружена, а во втором ее нет.

X Y						X Y
	- -	- -	- -	- - -

Имея корреляционную таблицу, в каждой клетке которой указана частота некоторой пары значений Х и Y вычисляют величину С_xy:

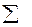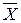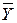C_xy = n_xy(x - )(y -)/n.

Величина C_xy носит название ковариации X и Y. Частное от деления величины C_xy на произведение средних квадратических отклонений величин S_x и S_y представляет собой выборочный коэффициент корреляции:

r_xy = C_xy / S_xS_y.

Для упрощения вычислений ковариации C_xy, а также S_x и S_y можно пользоваться следующими формулами:

C_xy = (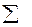x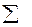n_xy y)/ n -;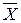

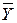S_x = ;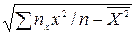

S_y = ;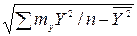

где n_x и m_y - частоты соответствующих значений x и y. Корреляционное отношение 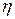_y вычисляется по формуле:

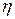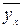_y = S/ S_y;

где S_y - среднее квадратическое отклонение значений y от средней ,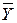

S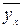 - среднее квадратическое отклонение значений частной средней 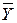_x от общей средней 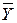, т.е.

S= .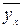

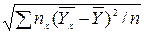Если на основании анализа коэффициента корреляции и корреляционного отношения установлено наличие прямолинейной корреляционной связи между Y и X, то эту связь можно выразить в виде следующего уравнения:

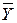_x - 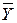= (r_xyS_y / S_x )(x - 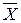) = b (x - 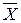); (7.1)

где b = r_xyS_y / S_x называется коэффициентом регрессии Y на X.

Уравнение (7.1) часто представляют в виде 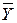_x = a + bx.

Если в результате расчета получено небольшое значение r_xy, то может возникнуть вопрос, не случайно ли значение r_xy отличается от нуля и не равен ли действительный коэффициент корреляции нулю. Этот вопрос разрешается сравнением численного значения r_xy с S_r. Приближенно можно считать, что среднее квадратическое отклонение S_r коэффициента корреляции r_xy численно равно

S_r = (1 - r) / .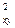

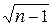Когда действительное значение коэффициента корреляции r_xy равно нулю, то

S_r= 1 / .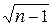

Поэтому, если

| r_xy | / S_r = | r_xy | 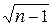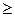3,

то можно считать r_xy значащим, а связь реальной, если же

| r_xy | 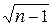< 3 ,

то можно предполагать, что линейная связь между переменными отсутствует, но возможна криволинейная.