После того, как установлено наличие связи между переменными строится, так называемое, корреляционное поле. Определяется эмпирическая линия регрессии. Выводится уравнение теоретической линии регрессии. Предположим, что в результате корреляционного анализа установлено равенство коэффициента корреляции корреляционному отношению. В этом случае вопрос решается простой подстановкой рассчитанных в процессе корреляционного анализа данных в уравнение (7.1). В случае, если такого равенства не наблюдается, необходим поиск криволинейной связи. Наиболее часто наблюдающейся в различных технических приложениях формой криволинейной связи является параболическая связь, выражающаяся уравнением параболы n –го порядка:
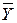 x = a + bx2 + cx3 +...
x = a + bx2 + cx3 +...
Задача заключается в поиске численных значений коэффициентов уравнения a,b,c,.... Метод, с помощью которого определяются коэффициенты уравнения, носит название метода наименьших квадратов.
Рассмотрим общую постановку вопроса. Пусть из каких либо соображений выбран общий вид функции Y = f (x), зависящий от нескольких числовых параметров a,b,c,...; именно эти параметры и требуется выбрать согласно методу наименьших квадратов так, чтобы сумма квадратов отклонений yi от f (x) была минимальна. Запишем y как функцию не только аргумента х, но и параметров a,b,c,...:
y = f (x;a,b,c,...).
Требуется выбрать a,b,c,... так, чтобы выполнялось условие:
 [ yi – f (x;a,b,c,...) ]2 = min (7.2)
[ yi – f (x;a,b,c,...) ]2 = min (7.2)
Найдем значения a,b,c,...,обращающие левую часть выражения (7.2) в минимум. Для этого продифференцируем eго по a,b,c,... и приравняем производные нулю:
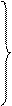
 [ yi –f (x;a,b,c,...) ] (
[ yi –f (x;a,b,c,...) ] (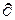 f /
f / 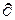 a)i = 0;
a)i = 0;
 [ yi –f (x;a,b,c,...) ] (
[ yi –f (x;a,b,c,...) ] (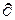 f /
f / 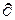 b)i = 0; (7.3)
b)i = 0; (7.3)
 [ yi –f (x;a,b,c,...) ] (
[ yi –f (x;a,b,c,...) ] (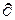 f /
f / 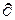 c)i = 0;
c)i = 0;
где (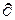 f /
f / 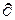 a)i = f/ (x;a,b,c,...) – значение частной производной функции f по параметру а в точке хi;
a)i = f/ (x;a,b,c,...) – значение частной производной функции f по параметру а в точке хi;
(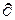 f /
f / 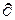 b)i, (
b)i, (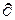 f /
f / 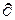 c)i,...- аналогично.
c)i,...- аналогично.
Система уравнений (7.3) содержит столько же уравнений, сколько неизвестных a,b,c,....
Решить систему (7.3) в общем виде нельзя; необходимо задаться конкретным видом функции f(x). Рассмотрим простейший случай нелинейной зависимости, когда корреляционная связь выражается уравнением параболы второго порядка:
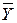 x = ax 2 + bx + c. (7.4)
x = ax 2 + bx + c. (7.4)
дифференцируя выражение (7.4) по a,b,c, получим:
(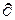 f /
f / 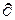 a)i = x
a)i = x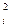 ; (
; (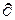 f /
f / 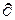 b)i = x i; (
b)i = x i; (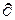 f /
f / 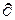 c)i = 1.
c)i = 1.
Подставляя производные в систему уравнений (7.3) имеем:
 [
[ 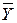 x
x – (ax2 + bx + c) ] 2 x
– (ax2 + bx + c) ] 2 x 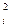 = 0,
= 0,
 [
[ 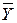 x
x – (ax2 + bx + c) ] 2 x i= 0,
– (ax2 + bx + c) ] 2 x i= 0,
 [
[ 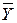 x
x – (ax2 + bx + c) ] 2 = 0,
– (ax2 + bx + c) ] 2 = 0,
После несложных преобразований получим систему уравнений:
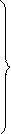
 x
x
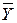 x
x = a
= a x
x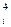 + b
+ b x
x + c
+ c x
x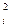 ,
,
 x i
x i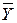 x
x = a
= a x
x + b
+ b x
x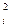 + c
+ c x i, (7.5 )
x i, (7.5 )

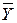 x
x = a
= a x
x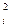 + b
+ b x i+ cn,
x i+ cn,
Решение системы уравнений (7.5) дает значение
коэффициентов a, b, c.
 2014-02-24
2014-02-24 607
607








