Приведем порядок (алгоритм) решения любой задачи (проблемы). 1. Ставится ФПЗ (физическая постановка задачи)

1. Ставится ФПЗ (физическая постановка задачи). Дано – найти. Цель.

2. Проводится обзор работ, патентно-информационный поиск (ПИП). Наброски математической модели.

3. Ставится МПЗ (математическая постановка задачи). Проводится анализ МПЗ.

4. Выбор и обоснование метода решения. АВМ, ЭЦВМ, эксперимент – что есть в наличии.

5. Решение задачи.

6. Анализ полученного решения

7. Выводы и рекомендации.

1.5 Стационарная теплопроводность

Рассмотрим наиболее простые случаи.

1.5.1. Теплопроводность плоской однослойной стенки

а) физическая постановка задачи. Пусть дана неограниченная плоская однослойная стенка толщиной d (Рис.1.5).

Рис. 1.5 Теплопроводность в плоской стенке

Пусть коэффициент теплопроводности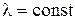. Известны температуры на левой поверхности t_п.1, а на правой – t_п.2, которые не изменяются со временем. Внутренние источники теплоты отсутствуют, т.е. q_V= 0. Тепловые потоки вдоль осей OY и OZ отстутсвуют. Тогда .

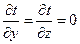Задача: Требуется найти распределение температур по сечению t(x) и тепловой поток q через стенку.

б) математическая постановка: для расчета процесса теплопроводности следует использовать дифференциальное уравнение (1.7) в декартовой системе координат. Заменим 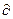на d, т.к. стенка плоская и температура зависит только от одной переменной х. Учтем, что температуры неизменны во времени, т.е.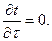

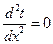; (1.15)

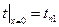; (1.16)

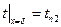. (1.17)

Система уравнений (1.15)…(1.17) представляет собой математическую постановку задачи теплопроводности в плоской стенке.

Решение диференциального уравнения (1.15): 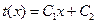; (1.18)

С помощью граничных условий (1.16) и (1.17) найдем постоянные 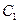и 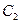. Полагая в уравнении (1.16) х=0, получим 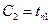, затем х=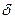в (1.17). Тогда .

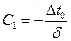Подставляя в (1.18) 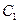и 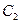, получим 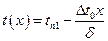, (1.19)

где ;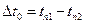

Анализ полученного решения.

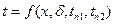. Температура согласно (1.19) меняется вдоль стенки по линейному закону.

Весьма удобно представить решение в безразмерном ви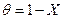де: , где 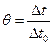, 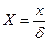; 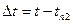, т.е. отсчет ведем от наименьшей температуры.

2) Тепловой поток согласно закону Фурье: ,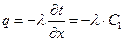

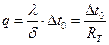, (1.20)

где 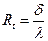м²К/Вт – термическое сопротивление плоской стенки.

3) 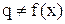. Другой вид решения (1.19)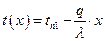

4) Полное количество теплоты 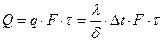, Дж.

5) Если учесть зависимость коэффициента теплопроводности, например, пусть 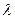изменяется по линейному закону 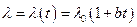, тогда решение будет иметь вид

,

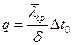где 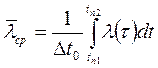- средний коэффициент теплопроводности.

Распределение температур 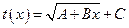– уже будет не прямая, а кривая линия (см. пунктирную линию на рис. 1.5.).