2014-02-24
556
.
Здесь оказалось, что количество не всегда пропорционально качеству, т.е. рост толщины изоляции не всегда уменьшает тепловые потери в окружающую среду.
Исследуем функцию термического сопротивления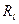 
на экстремум (Рис. 1.13). Для этого берем производную по диаметру изоляции и приравниваем ее нулю.
.
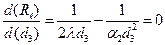Окончательно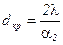 
. (1.31)
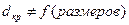
Если будет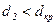 
то изоляция не эффективна. Должно быть: 
.
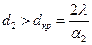Для других стенок, кроме плоской, можно получить аналогичные решения.
1.5.10. Теплопередача через шаровую стенку
Для шара: Поле температур t(r)= C1 - C2 /r. Тепловой поток:
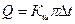,Вт, (1.40)
где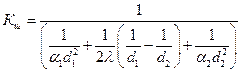 
; 
; 
.
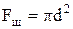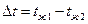Термические напряжения в шаровых стенках также определяется по уравнением (1.11) и (1.12). С учетом того, чтоб объем шара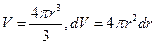 
уравнение (1.18) преобразуется к виду
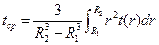. (1.41)
Подставляя в уравнение (1.44) решение (1.17) для поля температур в шаровой стенке в виде
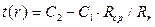, (1.42)
где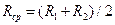 
- средний радиус стенки, м;
.
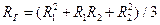При малых перепадах температур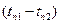 
: 
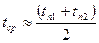
Способы усреднения поверхности нагрева:
- среднеарифметическое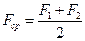 
;
- среднелогарифмическое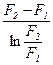 
; (1.33)
- среднегеометрическое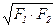 
;
где F1 – внутренняя, F2 – внешняя поверхность,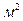 
.
Средняя температура поверхности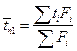 
; 
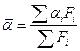–усредненный по поверхности коэффициент теплоотдачи. Тепловой поток 
.
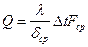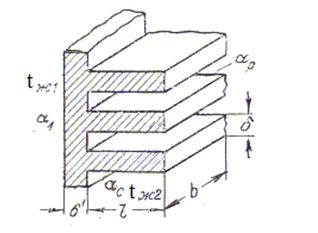
Рис. 1.14 Теплопередача через ребристую стенку
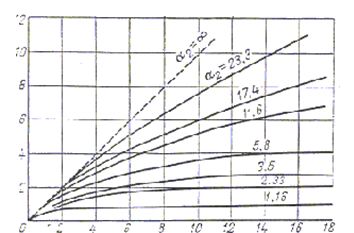
Рис. 1.15 Зависимость К=f (α1, α2)
