Рис. 2.1- К постановке задачи теплопроводности в пластине
Если пластина нагревается с одной стороны, а другая сторона изолирована, например, при нагреве заготовок, лежащих на подине печи, то ее можно рассматривать, как половину пластины; при этом изолированная сторона будет соответствовать середине пластины. Следовательно, за расчетную толщину пластины 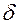 следует в этом случае принимать ее полную толщину.
следует в этом случае принимать ее полную толщину.
При рассмотрении процессов теплопроводности необходимо использовать дифференциальное уравнение переноса тепла. Так как тело плоское, используем дифференциальное уравнение теплопроводности в декартовой системе координат
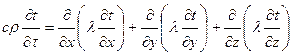 ,
,
где 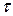 - время процесса, с;
- время процесса, с;
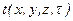 - искомая температура,
- искомая температура,  ;
;
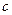 - массовая теплоёмкость, Дж/кг×К;
- массовая теплоёмкость, Дж/кг×К;
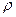 - плотность, кг/м3;
- плотность, кг/м3;
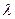 - коэффициент теплопроводности, Вт/м×К.
- коэффициент теплопроводности, Вт/м×К.
Для простоты задачу будем решать в линейной постановке, т. е. при постоянных, независящих от температуры теплофизических свойствах. Ввиду малости толщины пластины по сравнению с её высотой и шириной можно пренебречь осевыми 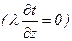 и продольными
и продольными 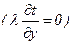 растечками тепла.
растечками тепла.
С учётом сказанного дифференциальное уравнение теплопроводности для данной задачи примет вид:
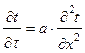 ,
, 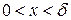 , (2.1)
, (2.1)
где 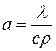 - коэффициент температуропроводности, м2/с.
- коэффициент температуропроводности, м2/с.
К уравнению (2.1) следует добавить краевые условия или условия однозначности:
— начальное условие
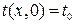 (2.2)
(2.2)
— и граничные условия на:
• левой 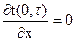 (2.3)
(2.3)
• правой границе 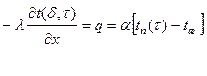 , (2.4)
, (2.4)
где 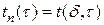 - температура на поверхности пластины,
- температура на поверхности пластины, 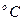 .
.
Уравнение (2.3) вытекает из условия симметрии или адиабатности на оси  (см. рис. 2.1).
(см. рис. 2.1).
Система дифференциальных уравнений (2.1)…(2.4) представляет собой математическую постановку рассматриваемой задачи.
Уравнение (2.1) является параболическим уравнением математической физики в частных производных, второго порядка. Поскольку дифференциальные уравнения (2.1)…(2.4), которые описывают процесс теплопроводности в теле простой формы линейные, можно получить точное аналитическое решение, применяя классический метод Фурье, т.е. метод разделения переменных [20].
Представим, что температура определяется произведением двух функций, одна из которых зависит только от пространственной координаты, а вторая - только от времени. Это эквивалентно введению следующей замены переменных:
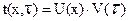 . (3.1)
. (3.1)
Дифференцируя (3.1) по времени и дважды по координате, а затем подставляя в уравнение (2.1), получим
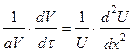 . (3.2)
. (3.2)
Известно, что две функции от двух разных и независящих друг от друга аргументов могут быть равны при любых значениях последних только в том случае, если они равны одной и той же постоянной величине, равной, например – k2. Тогда из выражения (3.2) вытекает два уравнения
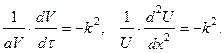
Решением последних будет
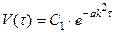 ,
,
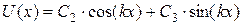 .
.
Подставляя U и V в уравнение (3.1), получим:
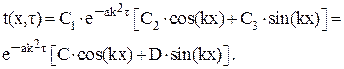 (3.3)
(3.3)
Постоянные интегрирования С, D и k находим из начального (2.2) и граничных условий (2.3) и (2.4). Подробный вывод приведён в [20].
Окончательно решение уравнения (3.3) в безразмерной форме, согласно [3] имеет вид:
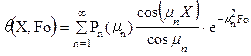 , (3.4)
, (3.4)
где 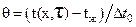 - безразмерная, относительная температура, 0≤θ≤1;
- безразмерная, относительная температура, 0≤θ≤1;
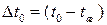 — первоначальная, максимально возможная разность температур, 0С;
— первоначальная, максимально возможная разность температур, 0С;
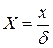 - безразмерная координата,
- безразмерная координата, 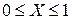 ;
;
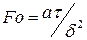 - безразмерное время, число Фурье;
- безразмерное время, число Фурье;
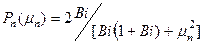 - тепловая амплитуда;
- тепловая амплитуда;
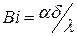 - число Био;
- число Био;
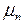 - характеристические числа, которые находятся из следующего трансцендентного уравнения:
- характеристические числа, которые находятся из следующего трансцендентного уравнения:
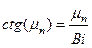 . (3.5)
. (3.5)
Из анализа уравнения (3.5) видно, что 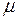 имеет бесчисленное множество значений. Наиболее просто можно определить корни уравнения (3.5) графическим путем. Если левую часть уравнения
имеет бесчисленное множество значений. Наиболее просто можно определить корни уравнения (3.5) графическим путем. Если левую часть уравнения 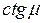 обозначить через
обозначить через 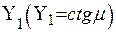 , а правую часть — через
, а правую часть — через 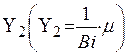 , то пересечения котангенсоиды
, то пересечения котангенсоиды 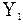 с прямой
с прямой 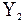 (рис. 3.1) дают нам значения корней
(рис. 3.1) дают нам значения корней 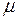 характеристического уравнения. Из рис. 3.1 видно, что имеется бесчисленное множество корней
характеристического уравнения. Из рис. 3.1 видно, что имеется бесчисленное множество корней 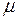 , причем каждое последующее решение больше предыдущего:
, причем каждое последующее решение больше предыдущего:
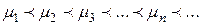
Чем больше n, тем ближе 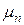 к числу
к числу 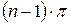 .
.
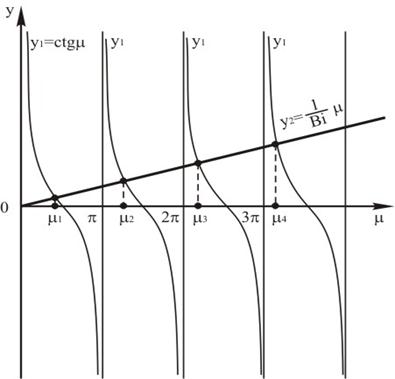
Рисунок 3.1- Графический способ определения корней характеристического уравнения
 2014-02-24
2014-02-24 536
536