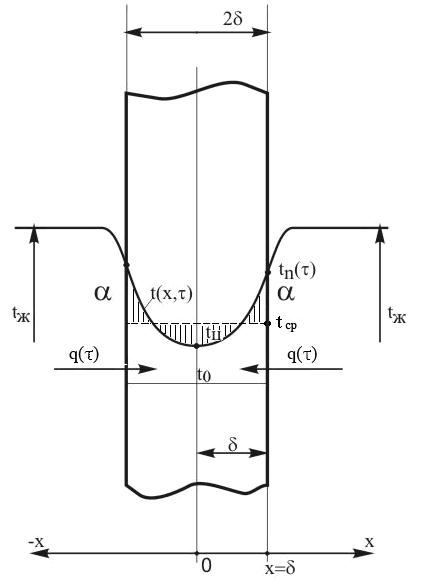
Дано:
Пластина толщиной 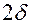 , гораздо меньшей её высоты и
, гораздо меньшей её высоты и  ширины с начальной равномерной (одинаковой) по толщине температурой
ширины с начальной равномерной (одинаковой) по толщине температурой 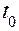 помещена в печь или другое пространство, имеющее постоянную температуру
помещена в печь или другое пространство, имеющее постоянную температуру 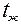 , и там нагревается при неизменном коэффициенте теплоотдачи
, и там нагревается при неизменном коэффициенте теплоотдачи 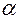 (рис. 2.1). Внутренние источники (стоки) тепла отсутствуют. Здесь и далее под жидкостью будем понимать как жидкость в буквальном смысле, так и газы.
(рис. 2.1). Внутренние источники (стоки) тепла отсутствуют. Здесь и далее под жидкостью будем понимать как жидкость в буквальном смысле, так и газы.
Требуется найти:
Температурное поле, т. е. температуры в любой момент времени в любой точке пластины, время нагрева её до заданной температуры поверхности 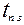 , количество тепла, пошедшего на нагрев и термические напряжения.
, количество тепла, пошедшего на нагрев и термические напряжения.
2.2. Математическая постановка задачи
Поместим начало координат на оси симметрии пластины. Вследствие
симметрии процесса нагрева будем искать температурное поле для правой половины пластины толщиной 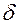 .
.
 2014-02-24
2014-02-24 505
505








