Непрерывность показательной функции

A). Докажем, что: .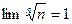

∆ Представим n в виде: . Затем раскроем скобки по биному Ньютона:

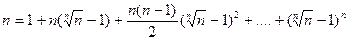. Тогда:

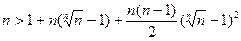Þ .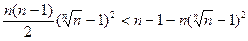

И получаем: 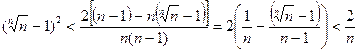Þ

Þ 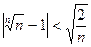. Выберем 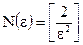. Получаем, что:

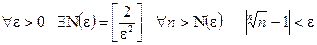т.е. . ▲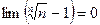

В). ∆ Теперь заметим, что пр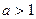и и : .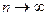

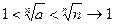Из принципа двустороннего ограничения заключаем, что:

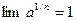Þ .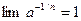

Следовательно:

,

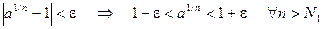и .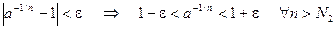

Тогда:

.

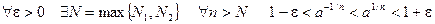И, наконец:

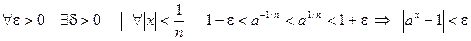
т.е. 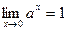. Полученное соотношение означает, что функция 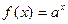непрерывна в нуле. ▲

С). ∆ =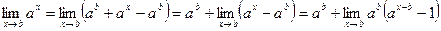

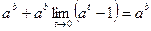= т.е. .

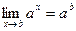Полученное равенство доказывает, что функция 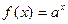непрерывна " x Î R. ▲