Т°. Если для двух последовательностей, из которых вторая строго монотонна и неограничена существует предел отношения приращений общих членов (конечный или равный +∞, -∞), то существует и равен этому пределу предел отношения общих членов последовательностей. 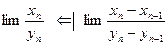 ∆ ▲.
∆ ▲.
Примеры:
1°. 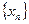 ;
; 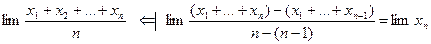 ;
;
2°. (a > 1); lim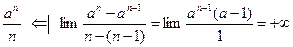 ;
;
3°. 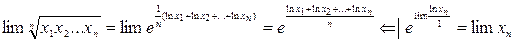 ;
;
4°. Для положительной последовательности, если существует предел отношения ее общего члена к предыдущему (конечный, равный +0, или равный +∞), то существует имеющий то же значение предел корня n -й степени из хn.
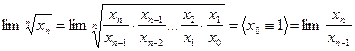 .
.
5°. 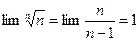 .
.
6°. 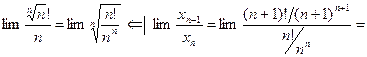
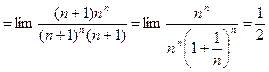 .
.
 2014-02-24
2014-02-24 1972
1972








