Верхние и нижние пределы последовательностей и функций

Def. Нижним пределом последовательности (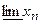) называется наименьший из частичных пределов этой последовательности. Верхним пределом последовательности (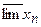) называется наибольший из частичных пределов последовательности.

При этом: ≤ .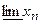

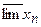Всякий частичный предел последовательности лежит между ее нижним и верхним пределами.

Т˚. Предел последовательности существует тогда и только тогда, когда ее верхний и нижний пределы совпадают.

Δ 1) Пусть 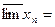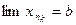и 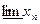= 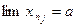и b>a.

——(—|—)———(—|—)——

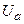
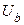
a b

$ N начиная с которого все элементы 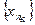и 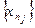попали соответственно в окрестност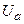и и 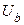. Тогда смешав элементы этих двух последовательностей получим последовательность, не имеющую предела. Следовательно, если верхний и нижний пределы последовательности не равны между собой, то существует подпоследовательность, не имеющая предела и, значит, предел последовательности не существует.

2) ▲

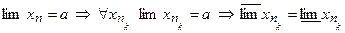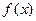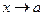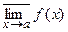У всякой функции, для которой aÎD (f)¢, существуют наибольший и наименьший частичные пределы. Они называются верхним и нижним пределами функции при : и .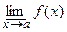

Т˚. Предел функци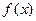и при 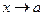существует тогда и только тогда, когда ее верхний и нижний пределы совпадают. Δ ▲.