
 1°. y = sin x
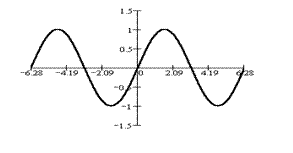
1°. y = sin x
Синусом числового аргумента называется синус угла в соответствующее число радиан. Синусом угла называется ордината конца подвижного радиуса, отвечающего заданному углу, на тригонометрическом круге (на круге единичного радиуса).
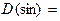 R;
R; 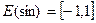 . Функция нечетная, периодичная с периодом Т = 2p.
. Функция нечетная, периодичная с периодом Т = 2p.
Ее график приведен выше.
Решение простейших уравнений: 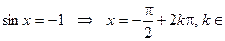 Z,
Z,
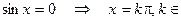 Z,
Z,
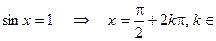 Z.
Z.
А уравнение 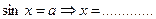 ?
?
На промежутке 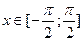 функция y = sin x монотонно возрастает и непрерывна.
функция y = sin x монотонно возрастает и непрерывна.
Следовательно, существует обратная к ней функция:
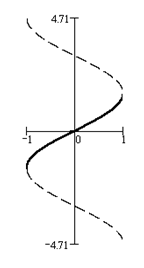
y = arcsin x. Справа приводим ее график.
Def. 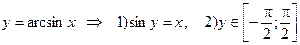 ;
;
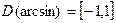 ,
, 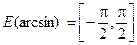 .
.
Отметим, что: 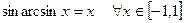
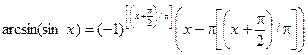
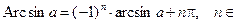 Z.
Z.
И тогда можно решить, приведенное выше простейшее уравнение:
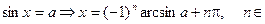 Z.
Z.
 2°. y = cos x
2°. y = cos x
Косинусом числового аргумента называется синус угла в соответствующее число радиан. Косинусом угла называется абсцисса конца подвижного радиуса, отвечающего заданному углу, на тригонометрическом круге (на круге единичного радиуса).
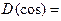 R;
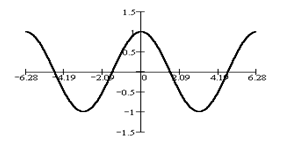
R; 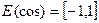 . Функция четная, периодичная с периодом Т = 2p.
. Функция четная, периодичная с периодом Т = 2p.
Ее график приведен выше.
Решение простейших уравнений: 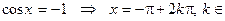 Z,
Z,
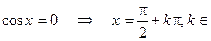 Z,
Z,
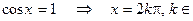 Z.
Z.
А уравнение 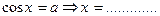 ?
?
На промежутке 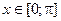 функция y = cos x монотонно убывает и непрерывна.
функция y = cos x монотонно убывает и непрерывна.
Следовательно, существует обратная к ней функция:
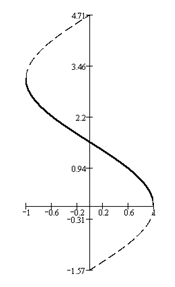
y = arccos x. Справа приводим ее график.
Def. 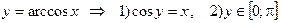 ;
;
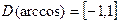 ,
, 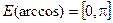 .
.
Отметим, что: 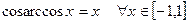
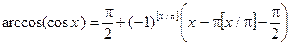
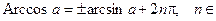 Z.
Z.
И тогда можно решить, приведенное выше простейшее уравнение:
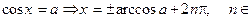 Z.
Z.
Приведем еще несколько полезных соотношений:

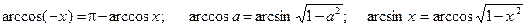 ;
;
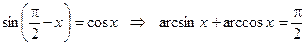 .
.
3. 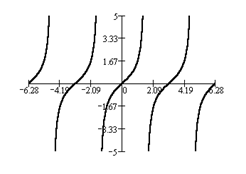 y = tg x
y = tg x
Тангенсом числового аргумента называется отношение синуса и косинуса того же аргумента. Его величина равна ординате точки пересечения продолжения радиуса подвижного круга с вертикальной прямой, проходящей через точку с координатами (1, 0) на тригонометрическом круге (эта прямая называется осью тангенсов).
D (tg) = R \{ x | x = 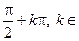 Z }; Е (tg) = R.
Z }; Е (tg) = R.
Функция нечетная, периодичная с периодом Т = p.
График функции приведен выше.
Решение простейших уравнений: tg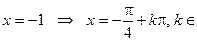 Z,
Z,
tg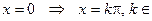 Z,
Z,
tg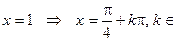 Z,
Z,
А уравнение tg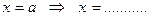 ?
?
 На промежутке
На промежутке 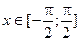 функция y = tg x монотонно возрастает и непрерывна.
функция y = tg x монотонно возрастает и непрерывна.
Следовательно, существует обратная к ней функция:
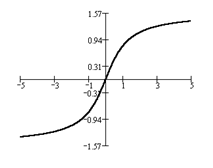
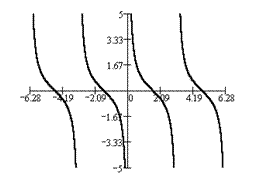
y = arctg x. Справа приводим ее график.
Def. 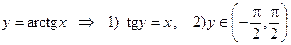 ;
;
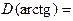 R, E (arctg) =
R, E (arctg) = 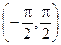 .
.
Отметим, что: 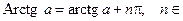 Z.
Z.
И тогда можно решить, приведенное выше простейшее уравнение:
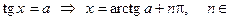 Z.
Z.
Приведем еще несколько полезных соотношений:
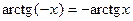
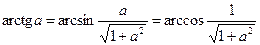 .
.
 4. y =ctg x
4. y =ctg x
Котангенсом числового аргумента называется отношение косинуса и синуса того же аргумента. Его величина равна абсциссе точки пересечения продолжения радиуса круга с горизонтальной прямой, проходящей через точку с координатами (0, 1) на тригонометрическом круге (эта прямая называется осью котангенсов).
D (сtg) = R \{ x | x = 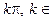 Z }; Е (сtg) = R.
Z }; Е (сtg) = R.
Функция нечетная, периодичная с периодом Т = p.
График функции приведен выше.
Решение простейших уравнений: сtg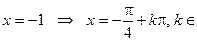 Z,
Z,
 сtg
сtg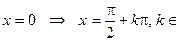 Z, сtg
Z, сtg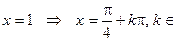 Z,
Z,
А уравнение сtg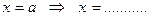 ?
?
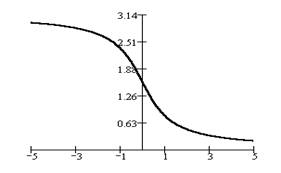
На промежутке 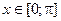 функция y = ctg x монотонно убывает и непрерывна.
функция y = ctg x монотонно убывает и непрерывна.
Следовательно, существует обратная к ней функция:
y = arcсtg x. Справа приводим ее график.
Def. 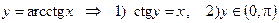 ;
;
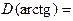 R, E (arctg) =
R, E (arctg) = 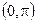 .
.
Отметим, что: 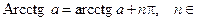 Z.
Z.
И тогда можно решить, приведенное выше простейшее уравнение:
с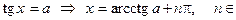 Z.
Z.
Приведем еще несколько полезных соотношений::
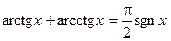 ,
,
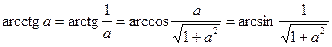 .
.
 2014-02-24
2014-02-24 638
638








