Каждая тригонометрическая функция имеет свой гиперболический аналог.
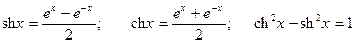 .
.
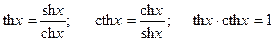 .
.
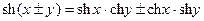 ,
, 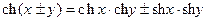 .
.
|
|
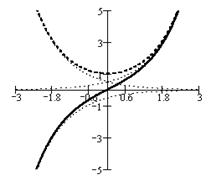
На рисунке слева приводятся графики гиперболических синуса (сплошная линия) и косинуса (пунктирная линия). Тонкой пунктирной линией построен график функции 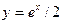 и симметричные ему относительно оси абсцисс и оси ординат.
и симметричные ему относительно оси абсцисс и оси ординат.
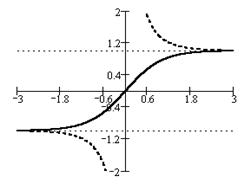
На рисунке справа приводятся графики гиперболических тангенса (сплошная линия) и котангенса (пунктирная линия). Тонкой пунктирной линией построен график функций  .
.
Для всех введенных гиперболических функций (для y = ch x отдельно для х > 0 и отдельно для x < 0) существуют обратные функции.
Найдем обратные функции к гиперболическим функциям:
1°. 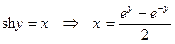 Þ
Þ 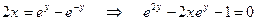 Þ
Þ
Þ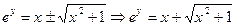 Þ
Þ 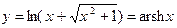 .
.
2°. 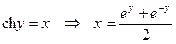 Þ
Þ 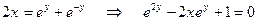 Þ
Þ
Þ 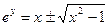 (
(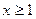 ) Þ
) Þ 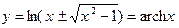 .
.
Получили две однозначные ветви обратной функции.
3°. 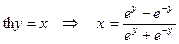 Þ
Þ 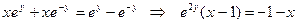
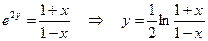 =
= 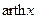 (если
(если 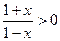 ).
).
4°. 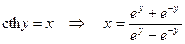 Þ
Þ 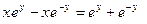 Þ
Þ 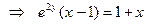 Þ
Þ 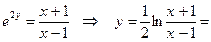
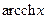 (если
(если 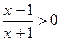 ).
).
5°. Из 3°. и 4°.: 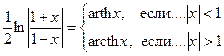 .
.
Ниже приводятся графики обратных гиперболических функций:
|
| ||||
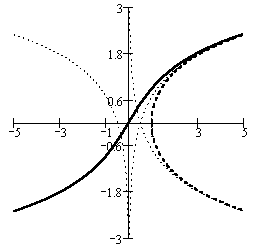
Слева приведены графики функций обратных гиперболическому синусу (сплошной линией) и косинусу (пунктирной линией), причем во втором случае приводятся обе ветви: одна выше а другая ниже оси абсцисс.
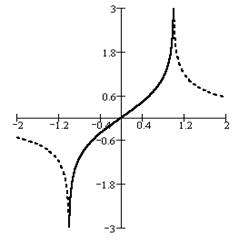
Справа приведены графики функций обратных гиперболическому тангенсу (сплошной линией) и котангенсу (пунктирной линией).
§. Равномерная непрерывность
Def. Функция 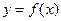 называется равномерно непрерывной на множестве Х, если
называется равномерно непрерывной на множестве Х, если
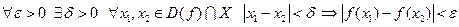 .
.
Из определения равномерной непрерывности функции на множестве следует, что функция непрерывна в каждой точке этого множества, но не наоборот.
Примеры:
1°. 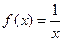 . Функция
. Функция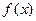 - непрерывна на
- непрерывна на 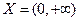 . Однако:
. Однако:
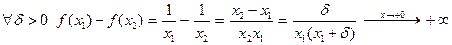 ,
,
т.е. 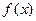 не является равномерно непрерывной на промежутке
не является равномерно непрерывной на промежутке 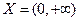 .
.
2°. 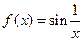 , Функция
, Функция 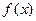 - непрерывна на
- непрерывна на 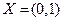 . Но, если положить
. Но, если положить
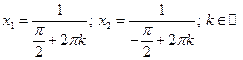 то получим:
то получим:
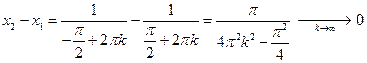 ,
,
и при этом: 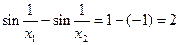 .
.
Из этого делаем заключение о том, что функция 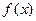 не является равномерно непрерывной на
не является равномерно непрерывной на 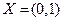 .
.
Т° Кантора (о равномерной непрерывности). Если функция непрерывна на замкнутом промежутке то она равномерно непрерывна на нём.
∆ Пустьфункция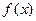 непрерывна на замкнутом промежутке
непрерывна на замкнутом промежутке 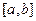 . Тогда:
. Тогда:
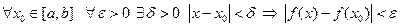 .
.
Множество всех дельта-окрестностей 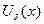 точек промежутка образует открытое покрытие замкнутого промежутка
точек промежутка образует открытое покрытие замкнутого промежутка 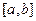 . Выделив из этого покрытия конечное подпокрытие получим:
. Выделив из этого покрытия конечное подпокрытие получим: 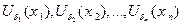 - конечное подпокрытие.
- конечное подпокрытие.
Положим 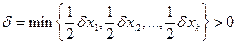 . Тогда:
. Тогда:
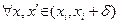
 Þ
Þ 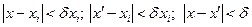 Þ
Þ
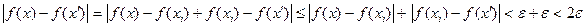 .
. ▲
▲
 2014-02-24
2014-02-24 1710
1710