Функциональные уравнения

Модуль непрерывности.

Def. Модулем непрерывности 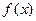на множестве Х называется:

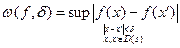
Т°. Функция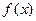равномерно непрерывна на множестве Х тогда и только тогда, когда её модуль непрерывности имеет предел равный нулю при .

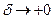1°. Задача: найти все непрерывные функции 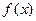, удовлетворяющие функциональному уравнению: .
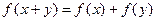а)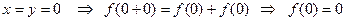
б)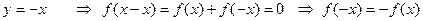

в)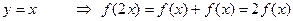

……………………………….

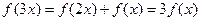
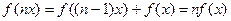
г) 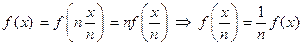; Тогда .

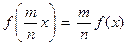Т.е. .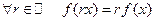

д) Пусть 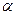- иррационально. Построим последовательность .

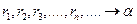Для нее, из непрерывности функции, получим: .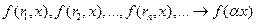

С другой стороны, из свойства г) следует, что: .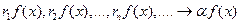

Из последних, двух равенств следует, что: .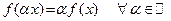
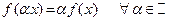е) В последнем равенстве положим .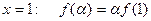

ж) Обозначая 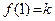, получаем искомое:

.
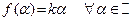Итак:

Единственной функцией определенной и непрерывной для 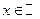и удовлетворяющей функциональному уравнению 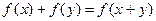является линейная однородная функция .

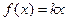Без вывода приведем еще ряд очень важных функциональных уравнений:

2°. ;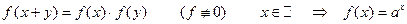

3°. ;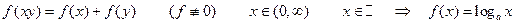

4°. ;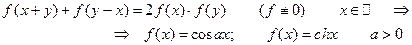

5°. .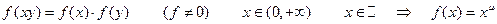

Эти функциональные уравнения впервые в непрерывных функциях были решены Коши.