в окрестности точки x 0 = 0.
Разложения функций в ряд Тейлора в окрестности точки x 0 = 0 называются разложениями в ряды Маклорена.
Множество значений х при которых ряд сходится называется областью сходимости ряда. Степенной ряд вида 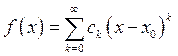 сходится в интервале
сходится в интервале 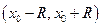 и R называется радиусом сходимости степенного ряда. В точках
и R называется радиусом сходимости степенного ряда. В точках 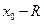 и
и 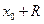 ряд может, как сходиться, так и расходиться. Радиус сходимости степенного ряда может быть найден по формулам:
ряд может, как сходиться, так и расходиться. Радиус сходимости степенного ряда может быть найден по формулам: 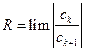 (формула Даламбера) или
(формула Даламбера) или 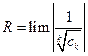 (формула Коши). По другому область сходимости ряда может быть установлена при оценке остаточного члена.
(формула Коши). По другому область сходимости ряда может быть установлена при оценке остаточного члена.
Более подробные сведения о рядах будут рассматриваться в последующем курсе.
Ниже следующие разложения получены по общей формуле разложения функции в ряд Тейлора.
1°. 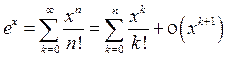 (x 0 = 0);
(x 0 = 0);
Оценим остаточный член, записав его в форме Лагранжа:
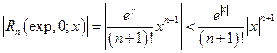 .
.
Из оценки следует, что при любом фиксированном х и n стремящемся к бесконечности остаточный член стремится к нулю, т.е. ряд сходится для любых х.
Тот же результат может быть получен из формулы Даламбера:
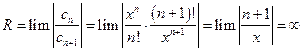 .
.
Область сходимости ряда х Î (–¥; +¥).
2°. 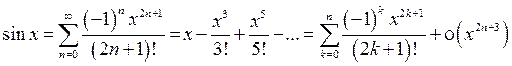 , (x 0 = 0).
, (x 0 = 0).
Оценка для остаточного члена:
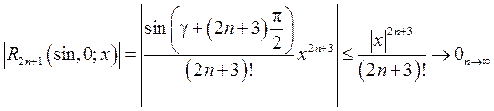 .
.
Область сходимости ряда х Î (–¥; +¥)
3°. 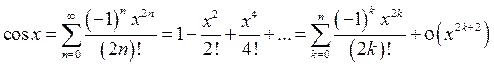 , (x 0 = 0).
, (x 0 = 0).
Оценка остаточного члена:
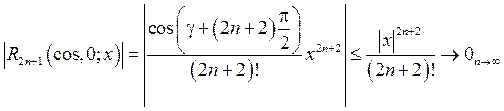 .
.
Область сходимости ряда х Î (–¥; +¥).
4°. 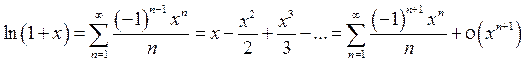 , (x 0 = 0).
, (x 0 = 0).
Оценка остаточного члена:
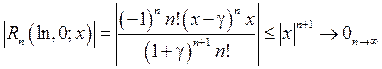 .
.
Если х = 1, то получается ряд 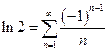 , который сходится по признаку Лейбница.
, который сходится по признаку Лейбница.
Область сходимости ряда х Î (-1, 1].
5°. 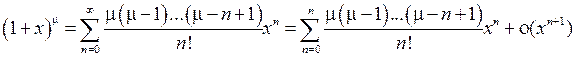 , (x 0 = 0).
, (x 0 = 0).
Для остаточного члена получаем:
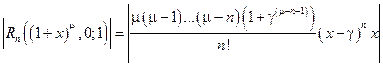 =
=
=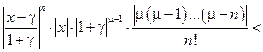
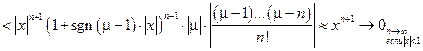 .
.
Область сходимости:
1) m Î N, x Î (–¥; +¥); 2) m > 0, x Î [–1; 1];
3) m Î (–1, 0), x Î (–1; 1]; 4) Общ. случай x Î (–1; 1).
 2014-02-24
2014-02-24 1156
1156








