Интегрирование простейших (элементарных) дробей

Элементарными дробями будем называть дроби следующих четырех типов:

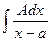I. ; II. , ;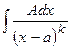

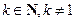III. 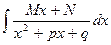; IV. , ;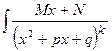

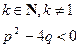Рассмотрим интегрирование указанных типов рациональных дробей.

Как видно интегралы первых двух типов это табличные интегралы.

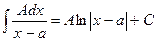I. ; II. .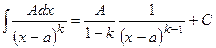

Теперь займемся интегралами третьего и четвертого типов.

III, IV. = = =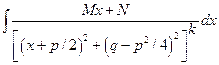

.

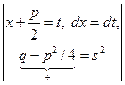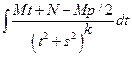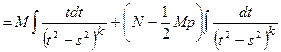Интегрирование первого интеграла не представляет трудностей.

а) ;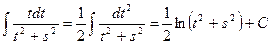

б) .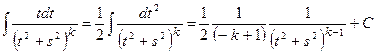

Интегрирование второго интеграла зависит от показателя степени в знаменателе.

в);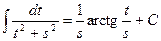

г) =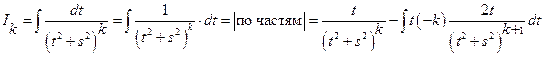

= .

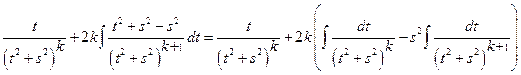Получено соотношение: 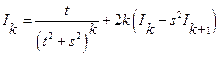, из которого

.

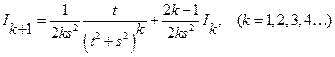Полученная формула понижения позволяет выразить 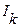через 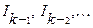и, в конце концов, через .

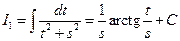Интегрирование указанных четырех типов рациональных дробей показывает, что они могут быть проинтегрированы, и в результате получится сумма рациональных функций), логарифмов, и арктангенсов. А в общем случае?