Примеры

1˚. Вычислить интеграл .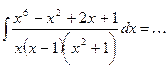

Рациональная подынтегральная дробь неправильная, поэтому выделим целую часть.

Т.к. 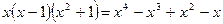, то 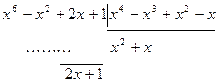и, значит

= .

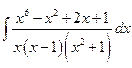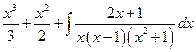Чтобы взять оставшийся интеграл, разложим дробь в сумму простейших:

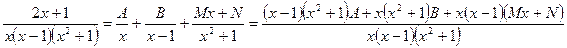
(A, B, M, N – неопределенные коэффициенты).

*. Две дроби с равными знаменателями равны тогда и только тогда, когда равны их числители.

= .

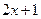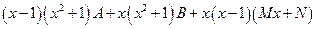* Два многочлена равны тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают. Из этого критерия и последнего равенства получаем:

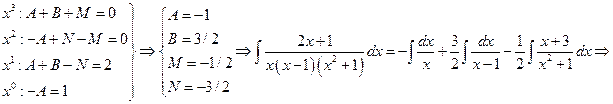
Получаем .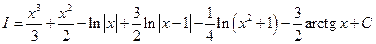

2˚. Вычислить интеграл .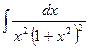

Разложим подынтегральную дробь в сумму простейших дробей:

,

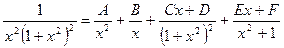и можно найти A, B, C, D, E, F как в предыдущей задаче, но…

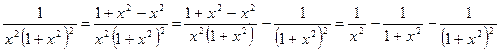
и, следовательно: .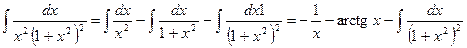

Оставшийся интеграл это интеграл четвертого типа 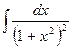и для его взятия можно использовать полученную выше формулу понижения.

.

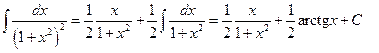В данном случае интеграл четвертого типа оказался не очень сложным. В общем случае, именно интегралы четвертого типа вызывают самые большие, хотя и технические, трудности. Избежать этих трудностей позволяет исключительно остроумный метод Остроградского.