2014-02-24
854
Многие задачи прикладной математики записываются в виде операторных уравнений
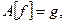(4.1)
где 
– известный линейный ограниченный оператор, биекция,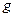 
– известная функция, 
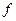– искомая функция.
Из биективности оператора следует существоание обратного оператора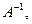 
а это значит, что существует единственное решение уравнения (4.1), которое выражается формулой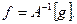 
В прикладных задачах бывает так, что функция 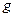получена в результате какого-то эксперимента и поэтому имеется только ее приближенное значение: 
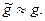Таким образом, вместо уравнения (4.1) реально решается уравнение
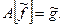(4.2)
Если, несмотря на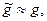 
решение 
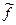уравнения (4.2) сильно отличается от решения 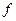уравнения (4.1), то это плохо, потому что это означает, что правую часть уравнения (4.1) нельзя заменить на приближенное значение: нельзя аппроксимировать более простыми функциями, нельзя задать значениями в нескольких узловых точках и т.д.. Поэтому естественное требование к уравнению (4.1) заключается том, что из 
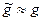должно следовать 
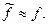Это означает, что необходимо потребовать непрерывность оператора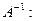 
|
|
|
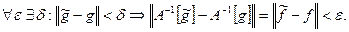
Говорят, что операторное уравнение (4.1) корректно разрешимо, если линейный оператор непрерывно обратим, т.е. существует обратный оператор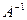 
и он непрерывен (=ограничен).
Приведем без доказательства две теоремы о непрерывной обратимости линейного оператора.
Теорема 4.3 (Банаха)
Пусть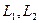 
– банаховы пространства, 
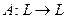– линейный ограниченный оператор, биекция. Тогда оператор непрерывно обратим.
Теорема 4.4 (о непрерывной обратимости оператора, близкого к тождественному)
Пусть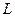 
– банахово пространство, 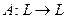– линейный ограниченный оператор, 
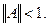Тогда линейный оператор 
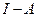непрерывно обратим и
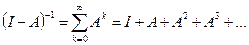
Параграф 5. Спектр линейного оператора
