Задание: для линейного оператора 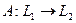 найти
найти 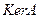 и
и 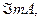 сделать выводы о существовании левого и правого обратного операторов, построить их, если они существуют.
сделать выводы о существовании левого и правого обратного операторов, построить их, если они существуют.
1. 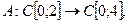
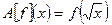
Это оператор замены переменной, причем функция 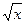 взаимно-однозначно отображает промежуток
взаимно-однозначно отображает промежуток 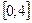 в
в 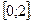 Ясно, что
Ясно, что 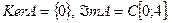 Следовательно, существует и левый, и правый обратный, т.е. просто обратный оператор
Следовательно, существует и левый, и правый обратный, т.е. просто обратный оператор 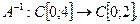 который сопоставляет каждой функции
который сопоставляет каждой функции 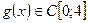 функцию
функцию 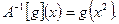 Проверим, что построенный оператор действительно является обратным:
Проверим, что построенный оператор действительно является обратным:
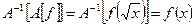
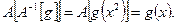
2. 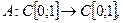
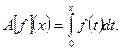
Найдем ядро оператора. Заметим, что 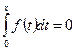 для любого
для любого 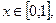 только если
только если 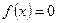 почти всюду на отрезке
почти всюду на отрезке 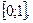 а поскольку
а поскольку 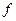 – непрерывная функция, то
– непрерывная функция, то 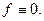 Следовательно,
Следовательно, 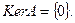
Найдем образ оператора. Если 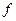 – непрерывная функция на отрезке
– непрерывная функция на отрезке 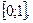 то
то 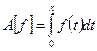 – непрерывно дифференцируемая функция, т.к. ее производная равна
– непрерывно дифференцируемая функция, т.к. ее производная равна 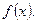 Кроме того, заметим, что
Кроме того, заметим, что 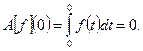 Значит, множество значений оператора
Значит, множество значений оператора  – это не все функции пространства
– это не все функции пространства 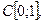 а только те, которые непрерывно дифференцируемы и принимают нулевое значение в точке
а только те, которые непрерывно дифференцируемы и принимают нулевое значение в точке 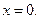 Следовательно,
Следовательно, 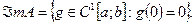
Поскольку 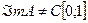 то представим оператор
то представим оператор  в виде
в виде 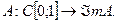 тогда для него существует и левый, и правый обратный, т.е. просто обратный оператор
тогда для него существует и левый, и правый обратный, т.е. просто обратный оператор 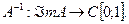 Нетрудно догадаться, что оператор
Нетрудно догадаться, что оператор 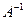 сопоставляет каждой функции
сопоставляет каждой функции 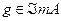 функцию
функцию 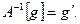
Проверим, что построенный таким образом оператор 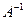 действительно является обратным к оператору
действительно является обратным к оператору 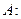
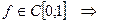
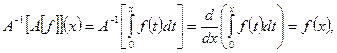
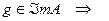
 2014-02-24
2014-02-24 544
544








