Определение 3.1

Пусть 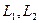– линейные нормированные пространства над полем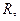 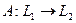– линейный оператор.

На языке 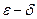: оператор непрерывен, если

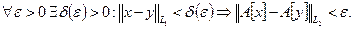
На языке последовательностей: оператор непрерывен, если

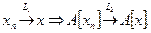
В конечномерных пространствах любой линейный оператор непрерывен, в бесконечномерных пространствах – не любой.

Теорема 3.2 (равносильность непрерывности и ограниченности для линейного оператора)

Пусть 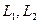– линейные нормированные пространства над полем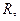 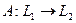– линейный оператор. Оператор непрерывен тогда и только тогда, когда он ограничен.

Доказательство

1. Докажем, что если линейный оператор ограничен, то он непрерывен. Пусть ограничен и пусть 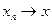в пространстве 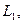покажем, что 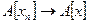в пространстве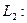

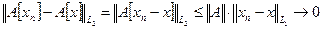при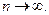

В этой цепочке соотношений последовательно использовали линейность оператора и свойство (2.1) ограниченного оператора.

2. Докажем, что если линейный оператор непрерывен, то он ограничен. Пусть непрерывен и допустим, что он не ограничен, чтобы прийти к противоречию.

Рассмотрим 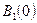– единичный шар с центром в нуле в пространстве 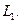Неограниченность оператора означает, что множество 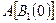неограничено в пространстве 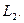Рассмотрим 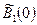– единичный шар с центром в нуле в пространстве 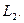Ясно, что 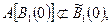иначе множество 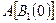было бы ограничено. По этой же причине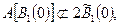 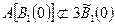и т.д. (см.рис.). Пользуясь этим наблюдением, выберем последовательность точек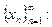

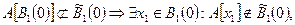
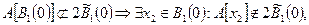
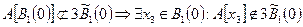и т.д..

Таким образом построена последовательность 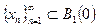такая, что или, что то же самое, При этом 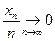в пространстве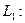 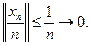В таком случае из непрерывности оператора следует, что 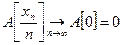в пространстве 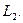Но это невозможно, так как Пришли к противоречию.