Определение 1.2

Ограниченный линейный оператор

Пусть 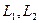– линейные нормированные пространства над полем 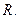Линейный оператор 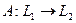называется ограниченным, если

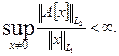
Символом 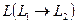будем обозначать множество всех линейных органиченных операторов. В этом множестве можно ввести структуры линейного пространства и нормированного пространства.

Определим поточечные операции сложения операторов и умножения оператора на вещественное число. Положим для любых 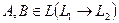и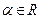

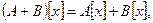
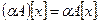
Вместе с этими операциями множество 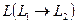является линейным пространством над полем 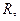аксимомы 1) – 8) линейного пространства проверяются элементарно. Роль нулевого элемента играет нулевой оператор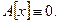

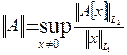
Назовем нормой линейного ограниченного оператора величину, использованную в определении 1.2:

Упражнение: проверить для операторной нормы выполнение аксиом I – III.

Упражнение: проверить, что норма нулевого оператора равна нулю, норма тождественного – равна 1.

Таким образом, линейное пространство 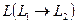вместе с введенной нормой является нормированным пространством.

Параграф 2. Техника вычисления операторной нормы

Из определения 1.2 операторной нормы вытекает важное соотношение:

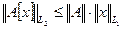для любого 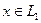, (2.1)

причем 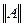– наименьшая из возможных констант в этом неравенстве.

Отсюда вытекают два рецепта для оценивания и вычисления операторной нормы:

1) Чтобы оценить сверху значение операторной нормы, надо для получить соотношение типа 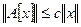для любого 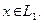Тогда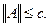

2) Чтобы вычислить точное значение операторной нормы, надо, кроме того, найти 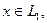на котором достигается равенство 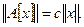Тогда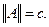

Приведем примеры получения оценки сверху или точного значения операторной нормы.

1. Рассмотрим оператор, действующий в пространствах последовательностей:

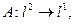
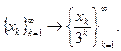
Найдем точное значение нормы этого линейного оператора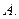

Оценим значение 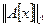через величину 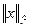с помощью неравенства Коши – Буняковского для сумм (см.раздел II соотношение (3.5)).

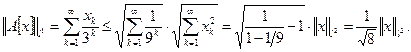
Таким образом, 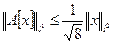для любого 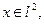а значит,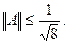

Неравенство Коши – Буняковского обращается в равенство для пропорциональных последовательностей, в частности, для равных, поэтому рассмотрим 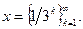Для такой последовательности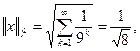 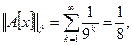следовательно, 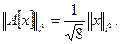Отсюда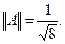

2. Рассмотрим оператор умножения и замены переменной, действующий в пространствах непрерывных функций:

,

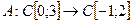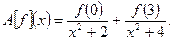
Найдем точное значение нормы этого линейного оператора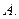

Оценим значение 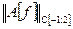через величину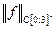

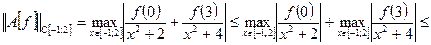
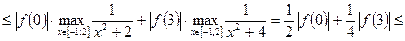
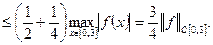
Таким образом, 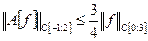для любой функции 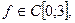а значит,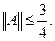

При 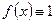получаем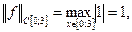 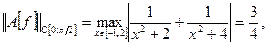следовательно, 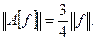Отсюда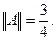

3. Рассмотрим интегральный оператор Фредгольма с интегрируемым ядром, действующий в пространствах непрерывных функций:

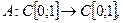
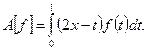
Оценим сверху значение нормы этого линейного оператора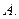

Оценим значение 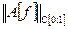через величину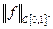

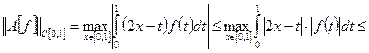
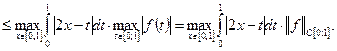
Осталось вычислить значение 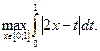Выражение 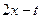при 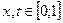принимает как положительные, так и отрицательные значения:

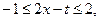
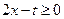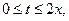
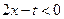при

при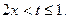

Тогда

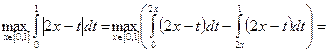
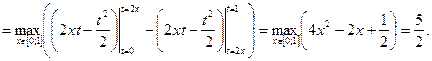
Таким образом, 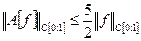для любой функции 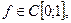а значит,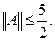

В данном случае представляется сложным найти точное значение операторной нормы. Оценка 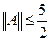не точна.

4. Рассмотрим оператор умножения и замены переменной, действующий в пространствах суммируемых функций:

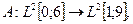
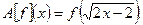
Оценим сверху значение нормы этого линейного оператора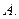

Оценим значение 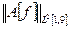через величину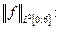

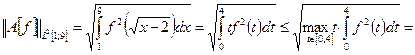
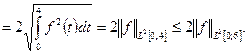
Таким образом, 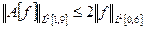для любой функции 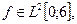а значит,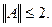

Параграф 3. Непрерывность линейного оператора