2014-02-24
362
Пусть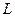 
– банахово пространство над полем 
, 
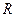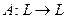– линейный оператор. Рассмотрим оператор вида 
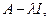где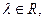 
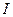– тождественный оператор. Спектом оператора 
называется множество таких чисел 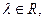для которых оператор 
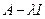не обратим. Обозначение для спектра: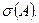 
Дополнение к спектру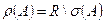 
называется резольвентным множеством оператора 
.
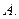Если линейный оператор ограничен, то его спектр и резольвентное множество обладают рядом полезных свойств, которые приводим без доказательства.
