Собственные функции симметричного оператора
Пусть 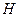 – гильбертово пространство над полем
– гильбертово пространство над полем 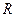 ,
, 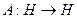 – линейный оператор, который определен на всем пространстве
– линейный оператор, который определен на всем пространстве 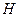 или на всюду плотном подпространстве
или на всюду плотном подпространстве 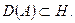 Оператор
Оператор  называется симметричным на своей области определения, если
называется симметричным на своей области определения, если
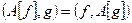 для любых
для любых 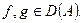
Приведем примеры симметричных операторов:
1. Рассмотрим оператор в конечномернм пространстве 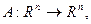
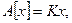 где
где 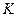 –матрица размера
–матрица размера 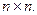 Он симметричный, если матрица
Он симметричный, если матрица 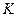 симметричная.
симметричная.
2. Рассмотрим интегральный оператор Фредгольма 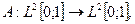
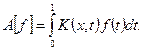 Он симметричный, если его ядро симметрично, т.е.
Он симметричный, если его ядро симметрично, т.е. 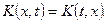
3. Рассмотрим дифференциальный оператор
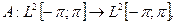
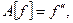
определенный на подпространстве 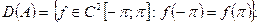 Дважды применяя интегрирование по частям, докажем, что линейный оператор
Дважды применяя интегрирование по частям, докажем, что линейный оператор  симметричный на своей области определения:
симметричный на своей области определения:
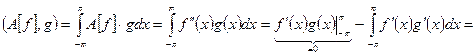
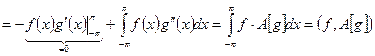 для любых
для любых 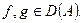
4. Рассмотрим дифференциальный оператор
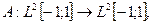
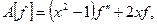
определенный на подпространстве 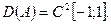 Как и в предыдущем примере, докажем его симметричность с помощью интегрирования по частям:
Как и в предыдущем примере, докажем его симметричность с помощью интегрирования по частям:
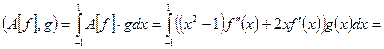
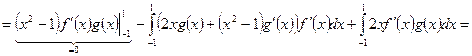
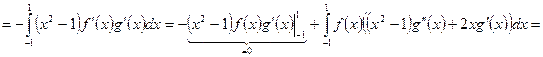
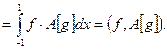
Теорема 5.3 (о спектральном разложении симметричного оператора)
Пусть 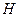 – гильбертово пространство над полем
– гильбертово пространство над полем 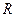 ,
, 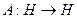 – симметричный линейный оператор. Тогда его собственные элементы (вектора, функции), соответствующие различным собственным значениям, ортогональны друг другу.
– симметричный линейный оператор. Тогда его собственные элементы (вектора, функции), соответствующие различным собственным значениям, ортогональны друг другу.
В частности, собственные вектора симметричного оператора могут образовывать ортонормированный базис в пространстве 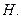 Например, собственные вектора оператора из примера 3 (см.выше) образуют полную тригонометрическую систему функций в пространстве
Например, собственные вектора оператора из примера 3 (см.выше) образуют полную тригонометрическую систему функций в пространстве 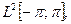 а собственные вектора из примера 4 образуют полную систему ортогональных полиномов Лежандра.
а собственные вектора из примера 4 образуют полную систему ортогональных полиномов Лежандра.
Почему эта теорема называется теоремой о спектральном разложении симметричного оператора? Причина в следующем. Предположим, что 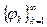 – ортонормированный базис в пространстве
– ортонормированный базис в пространстве 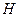 и
и 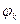 – собственная функция оператора
– собственная функция оператора  , соответствующая собственному числу
, соответствующая собственному числу 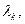 т.е.
т.е. 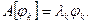 Тогда любую функцию
Тогда любую функцию 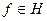 можно разложить в ряд Фурье
можно разложить в ряд Фурье 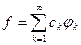 и действие оператора
и действие оператора  тоже представляется в виде ряда:
тоже представляется в виде ряда:
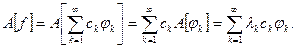 (5.1)
(5.1)
Разложение (5.1) и называется спектральным разложением симметричного оператора. Оно сильно упрощает жизнь при решении операторного уравнения
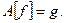 (5.2)
(5.2)
Пусть 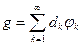 – разложение в ряд Фурье правой части уравнения (5.2), которая известна, следовательно коэффициенты
– разложение в ряд Фурье правой части уравнения (5.2), которая известна, следовательно коэффициенты 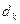 тоже известны. Ищем решение
тоже известны. Ищем решение 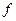 уравнения (5.2) в виде ряда
уравнения (5.2) в виде ряда 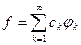 с неизвестными коэффициентами
с неизвестными коэффициентами 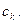 Подставляем эти разложения в уравнение (5.2). Благодаря соотношению (5.1) получается следующее равенство:
Подставляем эти разложения в уравнение (5.2). Благодаря соотношению (5.1) получается следующее равенство:
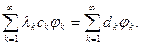
Приравнивая множители при одноименных 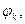 выражем отсюда искомые коэффициенты
выражем отсюда искомые коэффициенты
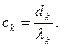
Таким образом, уравнение (5.2) может быть довольно сложным в зависимости от оператора 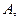 но решается очень просто, если оператор
но решается очень просто, если оператор  симметричный и его собственные функции образуют базис в пространстве
симметричный и его собственные функции образуют базис в пространстве 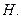
Параграф 6. Линейный функционал, сопряженное пространство
 2014-02-24
2014-02-24 389
389








