Пусть 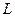 – линейное нормированное пространство над полем
– линейное нормированное пространство над полем 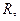 линейный оператор
линейный оператор  называется линейным функционалом.
называется линейным функционалом.
Линейный функционал – это частный случай линейного оператора, поэтому для него справедливо все то, что сообщали о линейных операторах предыдущие параграфы этого раздела.
Линейный функционал называется ограниченным, если 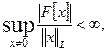 а число
а число  называется нормой линейного ограниченного функционала.
называется нормой линейного ограниченного функционала.
Множество всех линейных ограниченных функционалов обозначается символом  , оно является полным линейным нормированным пространством (короче, банаховым пространством) и называется сопряженным пространством к пространству
, оно является полным линейным нормированным пространством (короче, банаховым пространством) и называется сопряженным пространством к пространству 
Классическим примером линейного функционала является определенный интеграл:

Вычислим его норму:
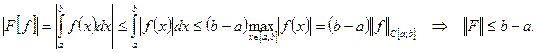
При  все неравенства в этой цепочке обращаются в равенства, поэтому
все неравенства в этой цепочке обращаются в равенства, поэтому 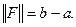
Теорема 6.2 (теорема Хана-Банаха о продолжении линейного функционала)
Пусть 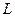 – линейное нормированное пространство,
– линейное нормированное пространство, 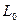 – замкнутое линейное подпространство
– замкнутое линейное подпространство 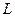 и пусть имеется линейный ограниченный функционал
и пусть имеется линейный ограниченный функционал 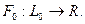 Тогда его можно продолжить на все пространство
Тогда его можно продолжить на все пространство 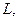 т.е. существует такой линейный ограниченный функционал
т.е. существует такой линейный ограниченный функционал 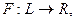 что
что 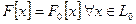 и
и 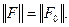
Теорема 6.3 (теорема Рисса о представлении функционала в гильбертовом пространстве)
Пусть 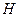 – гильбертово пространство,
– гильбертово пространство,  Тогда существует единственный элемент
Тогда существует единственный элемент 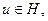 такой что
такой что  Причем
Причем 
Доказательство
Докажем существование такого представления.
Рассмотрим ядро линейного функционала 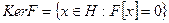 – линейное подпространство
– линейное подпространство 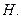 Если
Если  то это значит, что
то это значит, что 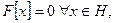 тогда положим
тогда положим 
Если 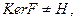 то
то 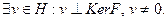 Используя линейность функционала
Используя линейность функционала 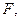 докажем, что
докажем, что 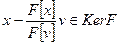 при любом
при любом 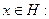
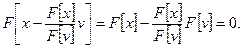
Тогда  а это значит, что
а это значит, что
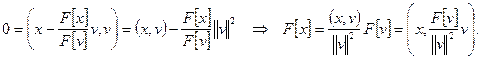
Осталось обозначить 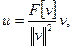 и представление линейного функционала в виде
и представление линейного функционала в виде 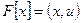 готово.
готово.
Докажем единственность этого представления.
Предположим, что 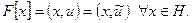 Тогда
Тогда  и в частности,
и в частности, 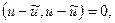 а это может быть только в случае
а это может быть только в случае 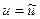 (см. первую аксиому скалярного произведения).
(см. первую аксиому скалярного произведения).
Докажем равенство норм 
Применяя неравенство Коши-Буняковского, получаем оценку для нормы функционала:
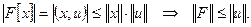
При 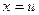 неравенство Коши-Буняковского обращается в равенство, поэтому
неравенство Коши-Буняковского обращается в равенство, поэтому 
Теорема доказана
В частности, теорема Рисса утверждает, что все линейные ограниченные функционалы в пространстве 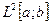 имеют вид
имеют вид 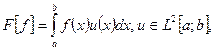 а все линейные ограниченные функционалы в пространстве
а все линейные ограниченные функционалы в пространстве 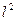 имеют вид
имеют вид 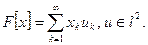
Рассмотрим пример применения теоремы Рисса для вычисления нормы линейного функционала в гильбертовом пространстве:
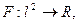
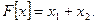
По теореме Рисса, должен существовать такой элемент 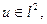 что
что  Нетрудно догадаться, что
Нетрудно догадаться, что  Тогда
Тогда 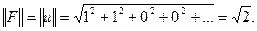
Следствие 6.4 теоремы Рисса
Любое гильбертово пространство 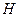 является самосопряженным, т.е.
является самосопряженным, т.е. 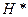 изоморфно
изоморфно 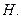
Изоморфизм строится элементарно: каждому функционалу 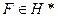 взаимо-однозначно сопоставляется элемент
взаимо-однозначно сопоставляется элемент 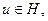 такой что
такой что 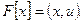
 2014-02-24
2014-02-24 834
834







