Напряжения

Классификация сил (модели нагружения)

При рассмотрении любой детали или сооружения взаимодействие с окружающими ее элементами и воздействие внешней среды характеризуется внешними силами. Классификация их представлена на рис.1.5.

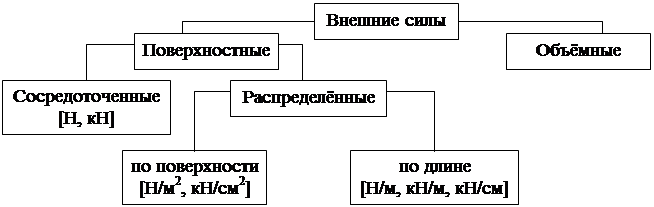Рис.1.5

1кгс = 9,81Н» 10Н; 1Н/м² = 1Па;

1тс = 9,8кН» 10кН; 10⁶Па = 1МПа.

Сосредоточенные силы – силы, действующие на небольших участках поверхности деталей (например, давление колеса на рельсы, давление моста на опору).

Распределённые силы – силы, приложенные к значительным участкам поверхности (например, давление жидкости или газа на стенки сосуда).

Объёмные или массовые силы – силы, приложенные к каждой частице материала (например, силы тяжести или силы инерции).

Важным моментом при разработке модели нагружения является учёт характера изменения внешних сил по времени. Классификация на рис.1.6.

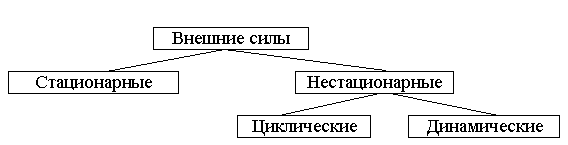
Рис.1.6

Стационарные или статические силы нагружают конструкцию медленно, постепенно возрастая от нуля до своего конечного значения. По достижении конечного значения не меняются. Ускорения элементов конструкций равны нулю.

Циклические или повторно – переменные нагрузки многократно меняют свою величину и направление по периодическому закону. Такие нагрузки испытывают вращающиеся валы машин.

Динамические нагрузки меняют свою величину в течение малого промежутка времени и сопровождаются значительными ускорениями, например, ударное нагружение, возникающее вследствие резкой остановки вращающегося массивного вала машины.

а б

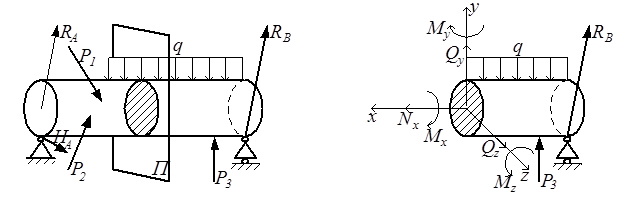
Деталь Отсечённая часть детали

Рис.1.7

Детали находятся в равновесии под воздействием приложенных к ним внешних сил (рис.1.7,а). Реакции опор также относятся к внешним силам. Взаимодействие между частями рассматриваемой детали характеризуется внутренними силами. Чтобы обнаружить внутренние силы, необходимо провести плоскость, которая рассечёт деталь на две части и рассмотреть равновесие любой из них (рис.1.7,б)

Внутренние силы в сечении П представляют собой силы взаимодействия между частицами материала. Из условий равновесия (1.1.) отсечённой части тела можно определить составляющие главного вектора и главного момента внутренних сил, действующих в сечении П. В этом состоит сущность метода сечения – одного из важных методов сопротивления материалов.

∑х = 0, ∑у = 0, ∑z = 0, ∑M_x = 0, ∑M_y = 0, ∑M_z = 0. (1.1)

Составляющие (компоненты) внутренних сил имеют следующие названия:

N_x – продольная сила;

Q_y и Q_z – поперечные силы;

M_x – крутящий момент;

M_y и M_z – изгибающие моменты.

Распределение внутренних усилий по сечению заранее неизвестно, определение его составляет одну из главных задач сопротивления материалов.

Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. Интенсивность внутренних сил измеряется напряжением.

Пусть на малую площадку ∆F, расположенную в окрестностях точки А сечения П, действует сила ∆P (рис.1.8).

а б

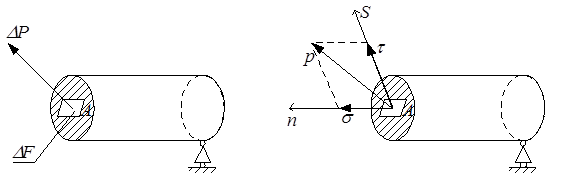
Сила в точке А Напряжения в точке А

Рис.1.8

Напряжение p в точке А рассматриваемого сечения определяется по формуле

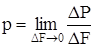. (1.2)

Вектор напряжения р совпадает с вектором усилия ∆Р. Как всякий вектор он может быть представлен нормальной (по отношению к площадке) составляющей σ и касательной составляющей τ (рис.1.8,б). Экспериментальными исследованиями установлено, что влияние нормальных и касательных напряжений на прочность различно, и поэтому в дальнейшем окажется необходимым всегда раздельно рассматривать составляющие вектора напряжений.

Итак, напряжение – это величина внутренней силы, приходящейся на единицу площади сечения в данной точке: σ – нормальное напряжение, τ – касательное напряжение, p – полное напряжение. Напряжение имеет размерность

.

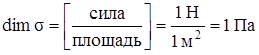Так как паскаль – очень маленькая величина, практические расчёты ведут в мегапаскалях или в килоньютонах на квадратный сантиметр: 10⁶ Па = 1 МПа, 10 МПа = 1 кН/см².

Напряжения в разных точках сечения могут быть различными. Величина напряжения меняется не только от точки к точке, но зависит и от ориентации площадки. Каждой площадке будет соответствовать определенное значение составляющих напряжений. Совокупность всех этих напряжений характеризует напряжённое состояние в точке.

1.5. Общие принципы расчёта на прочность

Целью расчёта является выяснение вопроса – удовлетворяет ли конструкция (деталь) требованиям надёжности, которые к ней предъявляются.

Надёжностью называется свойство изделия выполнять заданные функции, сохраняя свои эксплуатационные показатели в определённых пределах в течение требуемого промежутка времени или наработки,

Прочностной надёжностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции.

В машиностроении в качестве параметра работоспособности изделий, как правило, используют напряжение. Поэтому метод расчёта на прочность называется расчётом по допускаемым напряжениям. Порядок расчёта следующий:

1.Определение внешних нагрузок, составление расчётной схемы.

2.Определение внутренних усилий и характера их изменения. Нахождение положения опасного сечения.

3.Определение величины и характера распределения напряжений в опасном сечении. Нахождение опасной точки и определение величины наибольшего напряжения σ_max или, в случае сложного напряжённого состояния, величины наибольшего расчётного напряжения σ_расч.

4.Определение величины допускаемого напряжения [σ] по формуле

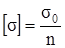, (1.3)

где σ₀ – опасное напряжение, соответствующее наступлению предельного состояния для данного материала, находится при лабораторных испытаниях;

n – запас прочности, n > 1.

5.Проверка условия прочности

σ_max ≤ [σ]. (1.4)

При определении допускаемого напряжения [σ] по формуле (1.3) очень важно правильно выбрать модель разрушения и обоснованно назначить запас прочности. Модель разрушения зависит от материала и условий нагружения детали. Может быть статическое разрушение, длительное статическое разрушение, усталостное разрушение, малоцикловое разрушение.

Глава 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ – СЖАТИЕ ПРЯМОГО БРУСА