1. Если при появлении события  событие
событие 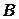 обязательно происходит, то говорят, что событие
обязательно происходит, то говорят, что событие  влечет событие
влечет событие 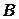 . Обозначение
. Обозначение 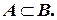
(Здесь и в дальнейшем будем пользоваться известными символами теории множеств).
Например,  - выпадение на верхней грани игральной кости числа очков, кратного 3, а
- выпадение на верхней грани игральной кости числа очков, кратного 3, а 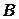 - выпадение числа очков, кратного 2. Тогда, случай
- выпадение числа очков, кратного 2. Тогда, случай 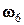 - выпадение на верхней грани числа очков равного 6, влечет событие
- выпадение на верхней грани числа очков равного 6, влечет событие  и событие
и событие 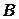 .
.
2. Говорят, что события  и
и 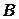 эквивалентны (равноправны) и пишут
эквивалентны (равноправны) и пишут  ~
~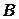 (или
(или 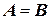 ) если
) если 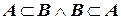 .
.
3. События  и
и 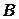 называются несовместными в данном испытании, если появление одного из них автоматически исключает появление другого. Впротивном случае события
называются несовместными в данном испытании, если появление одного из них автоматически исключает появление другого. Впротивном случае события  и
и 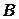 называются совместными. Другими словами, в результате испытания возможно их совместное осуществление, т. е. соответствующие множества
называются совместными. Другими словами, в результате испытания возможно их совместное осуществление, т. е. соответствующие множества  и
и 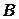 имеют общие элементы.
имеют общие элементы.
Например, при единичном бросании игральной кости событие  - выпадение грани с четным числом очков и событие
- выпадение грани с четным числом очков и событие 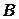 - выпадение грани с нечетным числом очков - н е с о в м е с т н ы, а событие
- выпадение грани с нечетным числом очков - н е с о в м е с т н ы, а событие 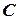 - выпадение числа очков, кратного 3 и
- выпадение числа очков, кратного 3 и  - выпадение числа очков, кратного 2 - с о в м е с т н ы, так как в пространстве элементарных исходов
- выпадение числа очков, кратного 2 - с о в м е с т н ы, так как в пространстве элементарных исходов 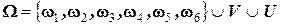 есть случай
есть случай 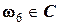 и
и 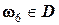 .
.
|
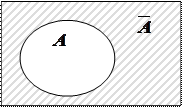
4. Противоположным событием 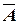 для события
для события  называется дополнение множества
называется дополнение множества  до
до 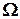 , т.е.
, т.е. 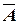 наступает при условии, что
наступает при условии, что  не происходит (
не происходит (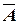 состоит из элементов
состоит из элементов  , не вошедших в
, не вошедших в  ). Другими словами,
). Другими словами, 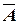 состоит в непоявлении
состоит в непоявлении  . Так, очевидно, что событие
. Так, очевидно, что событие 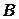 – выпадение грани с нечетным числом очков, является противоположным событием для события
– выпадение грани с нечетным числом очков, является противоположным событием для события  – выпадение грани с четным числом очков, то есть
– выпадение грани с четным числом очков, то есть 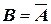 .
.
 2014-02-24
2014-02-24 4401
4401