Для доказательства теоремы Чебышева (да и других теорем, в том числе) воспользуемся одноимённым неравенством. Неравенство Чебышева (как впрочем и теорема) справедливо как для дискретных, так и для непрерывных случайных величин. Мы ограничимся, например, доказательством неравенства для непрерывной случайной величины.
НЕРАВЕНСТВО Чебышева [12]: Вероятность того, что отклонение случайной величины Х, имеющей конечную дисперсию 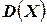 , от её математического ожидания по абсолютной величине на меньше любого положительного числа
, от её математического ожидания по абсолютной величине на меньше любого положительного числа 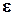 , ограничена сверху величиной
, ограничена сверху величиной 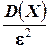 , то есть, справедливо неравенство:
, то есть, справедливо неравенство:
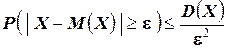 .
.
Доказательство: По определению дисперсии для непрерывной случайной величины можем записать
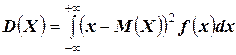 .
.
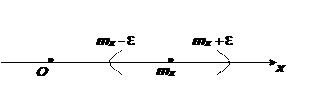
|
Выделим на числовой оси Ох 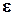 -окрестность точки
-окрестность точки 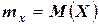 (см. рис.). Заменим теперь интегрирование по всей оси интегралом по переменной х на множестве
(см. рис.). Заменим теперь интегрирование по всей оси интегралом по переменной х на множестве 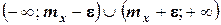 . Так как под знаком интеграла стоит неотрицательная функция[13], то результат интегрирования в результате может только уменьшиться, то есть
. Так как под знаком интеграла стоит неотрицательная функция[13], то результат интегрирования в результате может только уменьшиться, то есть
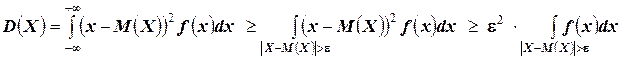 .
.
Интеграл в правой части полученного неравенства – это вероятность того, что случайная величина Х будет принимать значения вне интервала 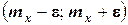 . Значит
. Значит
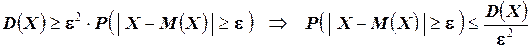 .
.
Неравенство доказано.
Замечание. Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто даёт грубую, а иногда и тривиальную (не представляющую интереса) оценку. Например, если 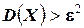 и, следовательно,
и, следовательно, 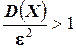 ; таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения находится в пределах от нуля до единицы, а это и без того очевидно, так как любая вероятность удовлетворяет этому условию.
; таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения находится в пределах от нуля до единицы, а это и без того очевидно, так как любая вероятность удовлетворяет этому условию.
Теоретическое же значение неравенства Чебышева весьма велико. Оценка, полученная Чебышевым, является универсальной, она справедлива для любых случайных величин, имеющих 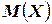 и
и 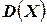 .
.
ПРИМЕР. Найти вероятность выхода случайной величины Х, имеющей математическое ожидание 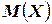 и дисперсию
и дисперсию 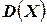 , за трёхсигмовые границы.
, за трёхсигмовые границы.
Решение. Воспользуемся неравенством Чебышева:
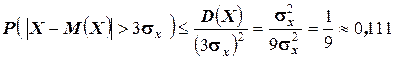 .
.
Сравним полученный результат с тем, который следует из правила трёх сигм для нормального закона распределения:
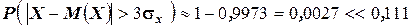 .
.
Нетрудно сделать ВЫВОД: случайные величины, встречающиеся на практике, чаще всего имеют значительно меньшую вероятность выхода за трёхсигмовые границы, чем 1/9. Для них область 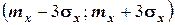 является областью практически возможных значений случайной величины.
является областью практически возможных значений случайной величины.
ТЕОРЕМА Чебышева (частный случай): Пусть Х 1 , Х 2 , …, Хn – попарно независимые случайные величины, имеющие одно и то же математическое ожидание М (Х), и пусть дисперсии этих величин равномерно ограничены (то есть не превышают некоторого постоянного числа С). Тогда, при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайных величин сходится по вероятности к их математическому ожиданию, то есть имеет место равенство:
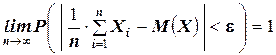 .
.
Доказательство. Применим к случайной величине 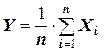 неравенство Чебышева:
неравенство Чебышева:
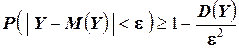 .
.
Заметим (по условиям теоремы), что для дисперсии 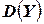 справедливы соотношения:
справедливы соотношения:
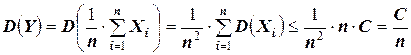 , то есть
, то есть 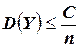 .
.
Тогда, согласно неравенству Чебышева
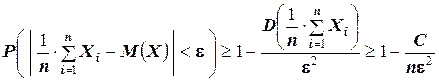 .
.
Переходя к пределу при 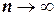 получаем
получаем
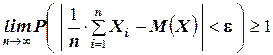 .
.
А так как вероятность не может быть больше единицы, то отсюда и следует утверждение теоремы.
Теорема Чебышева была обобщена на более общий случай, доказательство которой проводится аналогично доказательству, предложенному выше.
ТЕОРЕМА Чебышева (общий случай): Пусть Х 1 , Х 2 , …, Хn – попарно независимые случайные величины, и пусть дисперсии этих величин равномерно ограничены (то есть не превышают некоторого постоянного числа С). Тогда, при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий, то есть имеет место равенство:
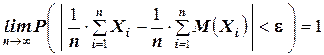 .
.
 2014-02-24
2014-02-24 6397
6397
