2014-02-24
1309
Центральная предельная теорема (Теорема Ляпунова)
Рассмотренные теоремы закона больших чисел касаются вопросов приближения некоторых случайных величин к определённым предельным значениям независимо от их закона распределения. В теории вероятностей, как уже отмечалось, существует другая группа теорем, касающихся предельных законов распределения суммы случайных величин. Общее название этой группы теорем – центральная предельная терема. Различные её формы различаются условиями, накладываемыми на сумму составляющих случайных величин. Впервые одна из форм центральной предельной теоремы была доказана выдающимся русским математиком А.М.Ляпуновым в 1900 году с использованием специально разработанного им метода характеристических функций.
ТЕОРЕМА Ляпунова: Закон распределения суммы независимых случайных величин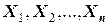 
приближается к нормальному закону распределения при неограниченном увеличении 
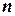(то есть, при 
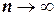), если выполняются следующие условия:
1. все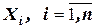 
имеют конечные математические ожидания и дисперсии: (
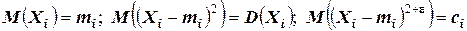, где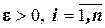 
);
|
|
|
2. ни одна из случайных величин по степени своего влияния на всю сумму случайных величин не отличается от остальных (то есть, влияние каждой из случайных величин на всю сумму ничтожно мало. Другими словами выполняется условие: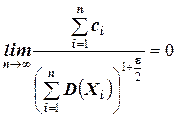 
).
Тогда
,
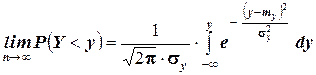где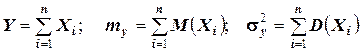 
.
Следует отметить, что центральная предельная теорема справедлива не только для непрерывных, но и для дискретных случайных величин. Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный (в частности, примером такой суммы может быть среднее арифметическое наблюдаемых значений случайных величин, то есть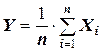 
).
Частным случаем центральной предельной теоремы является теорема Лапласа. В ней, как вы помните, рассматривается случай, когда случайные величины 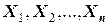дискретны, одинаково распределены и принимают только два возможных значения: 0 и 1.
Далее, вероятность того, что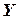 
заключено в интервале 
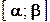можно вычислить по формуле
.
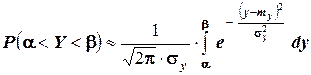Используя функцию Лапласа, последнюю формулу можно записать в удобном для расчётов виде:
,
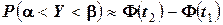где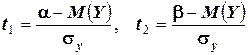 
.
ПРИМЕР. Пусть производится измерение некоторой физической величины. Любое измерение даёт лишь приближённое значение измеряемой величины, так как на результат измерения оказывают влияние очень многие независимые случайные факторы (температура, колебания прибора, влажность и др.). Каждый из этих факторов порождает ничтожную «частную ошибку». Однако, поскольку число этих факторов очень велико, совокупное их действие порождает уже заметную «суммарную ошибку».
|
|
|
Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок, мы вправе заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения.
