Связь между координатами одного и того же линейного оператора в разных базисах.
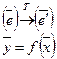
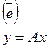
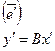
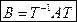
Т – матрица перехода от e к e’, то:
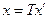
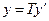

Если линейный оператор имеет в базисе невырожденную матрицу Т, матрица этого оператора в любом другом базисе не будет вырождена.
Если в базисе 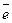 линейный оператор имеет матрицу А, а в базисе (
линейный оператор имеет матрицу А, а в базисе (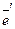 ) оператор имеет матрицу В
) оператор имеет матрицу В 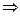
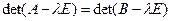
λ – произвольное число ≠0
Е – единичная матрица
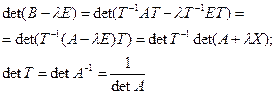
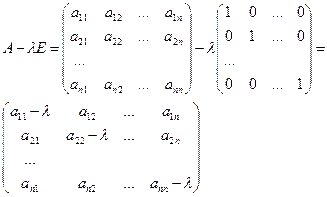 Если характеристически многочлен линейного оператора прировнять к 0, получим характеристическое уравнение линейного оператора.
Если характеристически многочлен линейного оператора прировнять к 0, получим характеристическое уравнение линейного оператора.
Собственные векторы линейного оператора
Ненулевой вектор 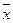 называется собственным вектором линейного оператора, если
называется собственным вектором линейного оператора, если 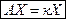 оператор к
оператор к 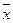 , получим этот же
, получим этот же 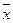 , умноженный на некоторое к.
, умноженный на некоторое к.
к – собственное число оператора А=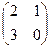
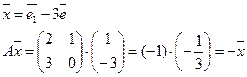
Каждый собственный вектор имеет единственное собственное число.
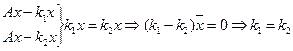
 2014-02-24
2014-02-24 1468
1468
