Определение 1. Одномерное проективное пространство Ф 1 называется проективной прямой.
В этом случае n=1, Ф n = Ф 1,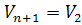 , то есть проективная прямая порождается двумерным векторным пространством (точнее его ненулевыми векторами).
, то есть проективная прямая порождается двумерным векторным пространством (точнее его ненулевыми векторами).
Рассмотрим две модели проективной прямой.
Первая модель. Пучок прямых с центром  на плоскости
на плоскости  .
.
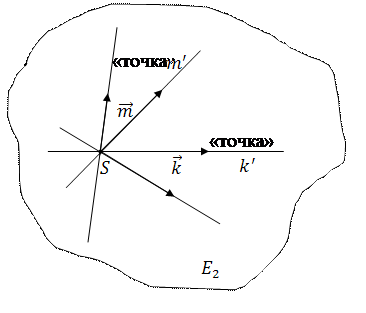
Точки проективной прямой Ф 1 изображаются прямыми 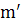 пучка с центром
пучка с центром 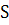 .
.
Векторы, порождающие эти точки, изображаются направляющими векторами 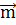 этих прямых
этих прямых 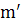 .
.
Вторая модель. Расширенная (пополненная) евклидова прямая 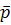 .
.
Точки проективной прямой Ф 1 – точки расширенной евклидовой прямой 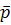 , как собственные, так и несобственная
, как собственные, так и несобственная 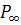 . Векторы, порождающие эти точки, по-прежнему есть направляющие векторы
. Векторы, порождающие эти точки, по-прежнему есть направляющие векторы 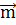 прямых
прямых 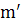 пучка с центром
пучка с центром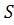 .
.
Выясним некоторые свойства проективной прямой с помощью её моделей.
 . Проективная прямая является линией замкнутой.
. Проективная прямая является линией замкнутой.
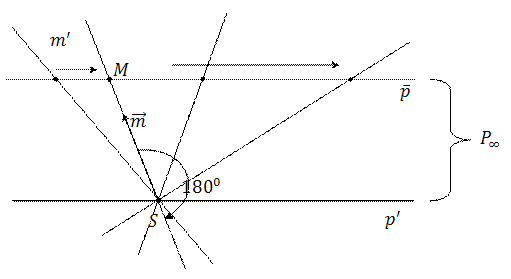
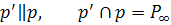
Если прямую 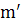 пучка с центром
пучка с центром  повернуть вокруг точки
повернуть вокруг точки  на
на 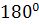 (в любом направлении), то она опишет весь пучок и вернётся в прежнее положение. При этом соответствующая ей точка
(в любом направлении), то она опишет весь пучок и вернётся в прежнее положение. При этом соответствующая ей точка 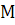 будет перемещаться по расширенной прямой
будет перемещаться по расширенной прямой 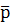 и вернётся в прежнее положение с противоположной стороны. Когда же прямая
и вернётся в прежнее положение с противоположной стороны. Когда же прямая 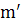 займёт положение прямой
займёт положение прямой 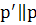 , точка
, точка 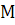 совпадёт с несобственной точкой
совпадёт с несобственной точкой 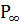 .
.
 . Две различные точки
. Две различные точки 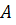 и
и 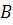 разбивают проективную прямую на две части.
разбивают проективную прямую на две части.
Точкам 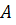 и
и 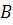 согласно аксиоме 4 в пучке прямых с центром
согласно аксиоме 4 в пучке прямых с центром  соответствуют две различные прямые
соответствуют две различные прямые  и
и  . Эти прямые образуют две пары вертикальных углов.
. Эти прямые образуют две пары вертикальных углов.
Остальные прямые пучка делятся на два множества: прямые, проходящие внутри одной пары этих углов и прямые, проходящие внутри другой пары вертикальных углов.
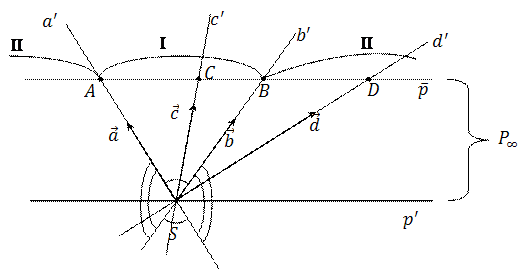
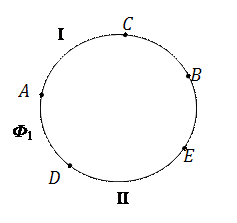
Соответственно этому точки 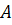 и
и 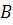 делят прямую
делят прямую 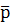 (модель проективной прямой Ф 1) на две части: часть I – обычный отрезок
(модель проективной прямой Ф 1) на две части: часть I – обычный отрезок 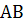 с исключёнными концами
с исключёнными концами 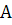 и
и 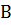 ; часть II – объединение двух лучей с началами в точках
; часть II – объединение двух лучей с началами в точках 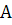 и
и 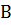 и точки
и точки 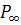 .
.
Определение 2. Два множества точек (I и II), на которые разбивается проективная прямая Ф 1 двумя различными точками 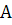 и
и 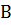 , ей принадлежащими, называются отрезками. Точки
, ей принадлежащими, называются отрезками. Точки 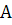 и
и 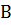 называются концами этих отрезков.
называются концами этих отрезков.
Если точки 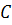 и
и 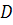 принадлежат различным отрезкам, то говорят, что пара точек
принадлежат различным отрезкам, то говорят, что пара точек 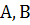 разделяет пару точек
разделяет пару точек 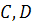 (или наоборот пара точек
(или наоборот пара точек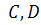 разделяет пару точек
разделяет пару точек 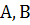 ).
).
Обозначение. 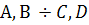 .
.
Замечание. Вследствие замкнутости проективной прямой для её точек теряет смысл отношение «лежать между», имеющее место для евклидовой прямой.
Вместо него взаимное расположение точек характеризуется отношением разделённости (или неразделённости) пар точек.
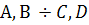 .
.
Напротив, пара точек 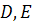 не разделяется парой точек
не разделяется парой точек 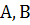 :
: 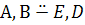 .
.
 2014-02-24
2014-02-24 2903
2903








