2014-02-24
1671
Глава 1. Понятие проективного пространства
Библиогр.: 19
Курс лекций
ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
И.С. Логунов
УДК 514. 144 (072.8)
ББК 22.151. 3 р 3
Л 698
Печатается по решению редакционно-издательского совета ФГБОУ ВПО «Орловский государственный университет».
Рецензент: кандидат физико-математических наук, доцент Панюшкин С.В.
Редактор: кандидат физико-математических наук, доцент Ломакин Д.Е.
Логунов И. С.ПРОЕКТИВНАЯ ГЕОМЕТРИЯ. – Орел: ОГУ, 2012. - 67 с.: илл.
Ó Логунов И. С., 2012 г.
Проективная геометрия возникла в первой половине XIX века. Основы её заложил в работе «Трактат о проективных свойствах фигур» известный французский математик Жан Виктор Понселе (1788-1867). Он выделил как объект изучения некоторые особые свойства геометрических фигур наиболее общего характера, которые назвалпроективными. Эти свойства связаны с понятием центрального проектирования.
Рассмотрим в евклидовом пространстве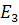 
две плоскост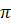и 
и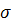 
и точку 
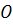, не лежащую на этих плоскостях. Пусть 
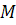– произвольная точка плоскости .
|
|
|
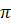Определение. Точка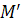 
пересечения прямой 
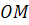с плоскостью 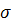называется проекцией точки 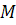на плоскость 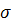из центра .
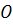Соответствие между точками 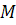плоскости 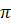и их проекциями 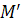на плоскость 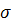называется центральным проектированием плоскости 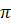на плоскость 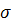из точки .
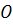Если 
– произвольная фигура плоскости 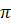, то множество проекций всех точек фигуры на плоскость 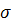является некоторой фигурой 
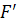плоскости 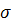, которая называется проекцией фигуры .
Изменяя положение точки 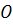и плоскости 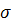, для одной и той же фигуры 
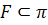будем получать различные фигуры 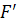. При этом многие свойства фигуры искажаются: например, меняются длины отрезков и величины углов, пересекающиеся прямые могут изображаться параллельными прямыми.
С другой стороны, некоторые свойства фигуры А сохраняются при любом центральном проектировании, например, свойство точек, лежащих на одной прямой или на одной линии второго порядка. Такие свойства фигур называются проективными. Изучением проективных свойств фигур и занимается проективная геометрия.
