Определение 1. Двумерное проективное пространство Ф 2 называется проективной плоскостью.
В этом случае n=2, Ф n = Ф 2, 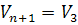 , то есть проективная плоскость порождается ненулевыми векторами трёхмерного векторного пространства.
, то есть проективная плоскость порождается ненулевыми векторами трёхмерного векторного пространства.
Рассмотрим две модели проективной плоскости.
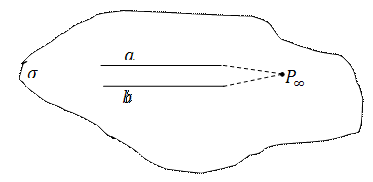
Первая модель. Связка прямых в трёхмерном евклидовом пространстве (с центром 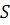 )
) 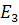 .
.
Точки проективной плоскости изображаются прямыми связки.
Векторы, порождающие эти точки, изображаются направляющими векторами этих прямых.
Прямые проективной плоскости изображаются пучками прямых с центром 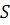 (см. первую модель проективной прямой). Каждый из таких пучков определяет некоторую евклидову плоскость
(см. первую модель проективной прямой). Каждый из таких пучков определяет некоторую евклидову плоскость 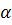 . Поэтому можно также сказать, что прямые проективной плоскости порождаются плоскостями связки с центром
. Поэтому можно также сказать, что прямые проективной плоскости порождаются плоскостями связки с центром  .
.
Вторая модель. Расширенная (пополненная) евклидова плоскость.
Каждую прямую евклидовой плоскости  дополним несобственной точкой, тем самым превратив эту прямую в расширенную евклидову прямую
дополним несобственной точкой, тем самым превратив эту прямую в расширенную евклидову прямую 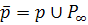 .
.
Будем считать также, что параллельные прямые дополняются одной и той же точкой:
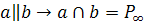
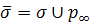
Определение 2. Евклидова плоскость 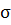 , дополненная несобственными точками
, дополненная несобственными точками 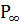 , называется расширенной евклидовой плоскостью и обозначается
, называется расширенной евклидовой плоскостью и обозначается 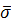 . Множество всех несобственных точек называется несобственной прямой
. Множество всех несобственных точек называется несобственной прямой 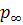 .
.
Между рассмотренными выше моделями проективной плоскости существует связь.
Определение 3. Соответствие между евклидовой плоскостью 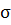 и связкой прямых с центром
и связкой прямых с центром 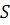 (евклидова трёхмерного пространства) называется перспективным, если каждой точке
(евклидова трёхмерного пространства) называется перспективным, если каждой точке 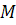 плоскости
плоскости 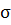 соответствует проходящая через неё прямая
соответствует проходящая через неё прямая 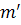 связки с центром
связки с центром 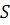 .
.
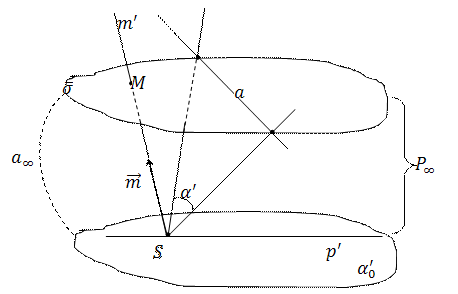
Если плоскость 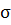 дополнена до расширенной плоскости
дополнена до расширенной плоскости 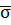 , то указанное перспективное соответствие становится однозначным (биективным). Прямым связки с центром
, то указанное перспективное соответствие становится однозначным (биективным). Прямым связки с центром 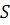 , не параллельным плоскости
, не параллельным плоскости 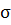 , соответствуют её собственные точки, а прямым
, соответствуют её собственные точки, а прямым 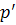 , параллельным плоскости
, параллельным плоскости 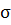 , соответствуют её несобственные точки.
, соответствуют её несобственные точки.
Прямой 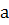 плоскости
плоскости 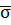 соответствует проходящая через неё плоскость
соответствует проходящая через неё плоскость 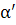 связки плоскостей с центром
связки плоскостей с центром 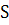 . Если
. Если 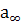 – несобственная прямая плоскости
– несобственная прямая плоскости 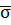 , то соответствующая ей плоскость
, то соответствующая ей плоскость 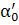 параллельна плоскости
параллельна плоскости 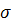 . Можно при этом считать, что эти две плоскости
. Можно при этом считать, что эти две плоскости 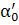 и
и 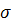 пересекаются по несобственной прямой
пересекаются по несобственной прямой 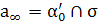 .
.
 2014-02-24
2014-02-24 4256
4256
