Группа проективных преобразований

Рассмотрим проективное отображение проективной плоскости P₂ на себя, то есть проективное преобразование этой плоскости (P₂’=P₂).

Как и прежде композицией f проективных преобразований f₁ и f₂ проективной плоскостиP₂ назовем результат последовательного выполнения преобразований f₁и f₂: f=f₂°f₁.

Теорема 1: множество H всех проективных преобразований проективной плоскости P₂ является группой относительно композиции проективных преобразований.

Доказательство:

1) Докажем, что композиция f любых двух проективных преобразований f₁ и f₂ также является преобразованием.

Пусть М – произвольная точка проективной плоскости P₂ и R=(e₁;e₂;e₃;e) – некоторая проективная система координат.

Преобразованиеf₁отображает точку Mна некоторую точку M’, а репер R – на некоторый репер R’=(e₁’;e₂’;e₃’;e’).

Преобразование f₂ отображает точку M’ на некоторую точку M”, а репер R’ – на некоторый репер R”=(e₁”;e₂”;e₃”;e”). Но тогда композиция f=f₂°f₁ отображает точку M на точку M’ и точку M’ на точку M”, то есть точку M на точку M”, а репер R на репер R”.

Так как f₁ и f₂ – проективные преобразования проективной плоскости P₂, то согласно определению 1 из §11 точки М и М’, а также M’ и M” имеют в системах координат R и R’, R’ и R” одинаковые координаты. Но тогда и точки М и M” имеют в системах координат R и R” одинаковые координаты

Таким образом, преобразование f=f₂°f₁ является проективным преобразованием проективной плоскости P₂.

2) Рассуждая аналогично, докажем, что преобразование f^-1, обратное проективному преобразованию f, также является проективным преобразованием проективной плоскости P₂.

3) Очевидно, тождественное преобразование е проективной плоскости P₂ является ее проективным преобразованием:

е: M (x₁:x₂:x₃)_R → M (x₁:x₂:x₃)_R’, где R’ – любой проективный репер проективной плоскости P₂.

Таким образом, множество Н всех проективных преобразований плоскости P₂ является группой относительно композиции проективных преобразований.

Определение 1: проективной геометрией называется раздел геометрии, изучающий не изменяющиеся при проективных преобразованиях свойства фигур. Другими словами, проективная геометрия – это наука об инвариантных проективных преобразованиях.

Примеры:

1) Прямолинейность расположения точек является инвариантом проективного преобразования согласно теореме из § 11;

2) Можно доказать, что отношение разделенности пар точек также является инвариантом проективного преобразования:

А, В ÷ С, D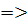A’, B’ ÷ C’, D’.

	C

Теорема 2: если проективное преобразование f проективной плоскости P₂ отображает точку M на M’, то координаты (x₁:x₂:x₃) точки М и координаты (x₁’:x₂’:x₃’) точки M’ в одной и той же проективной системе координат R=(e₁;e₂;e₃;e) связаны формулами:

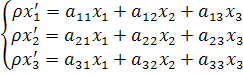
(1)

где 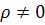– произвольный числовой множитель и det(a_ij) ≠ 0 (2)

Замечания: Справедлива и обратная теорема: «любое преобразование проективной плоскости, задаваемое формулами (1) при условии (2), является ее проективным преобразованием;

1) Формулы (1) похожи на формулы перехода от R к R’ на проективной плоскости, однако, они связывают координаты образа M’ и прообраза M при проективном преобразовании f в одной системе координат R, а не координаты одной точки в разных системах координат;

2) Коэффициенты a_ij(i, j=1, 2, 3) в формулах (1) определены с точностью до общего числового множителя;

3) Проективное преобразование проективной прямой Р₁ выражается в проетивных координатах формулами:

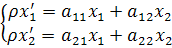
(3)

где 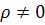и det(a_ij) ≠ 0 (4)

Определение 2: нетождественное проективное преобразование проективной плоскости Р₂, переводящее все точки некоторой прямой l в себя и имеющее точно одну неподвижную точку S, называется гомологией. Прямая l называется осью гомологии, точка S – центром гомологии.

Фигуры, полученные одна из другой при некоторой гомологии, называются гомологичными.

Свойства гомологии:

1. Прямые, соединяющие гомологичные точки, проходят через центр гомологии.

2. Гомологичные прямые пересекаются на оси гомологии.

3. Гомология задается осью l, центром S и парой соответственных точек.

Замечание 1: трехвершинники из теорем Дезарга являются гомологичными; центром гомологии является точка ДезаргаQ, осью гомологии – прямая Дезарга.

Примеры гомологии:

1) Центр – собственная точка S, ось – несобственная прямая l_∞.

'ямая несобственная

A_0∞, B_0∞, C_0∞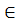l_∞

Гомотетия H^k_S, где .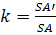

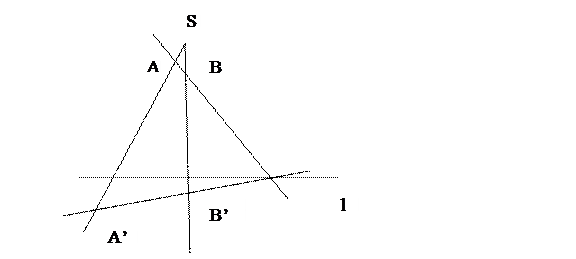
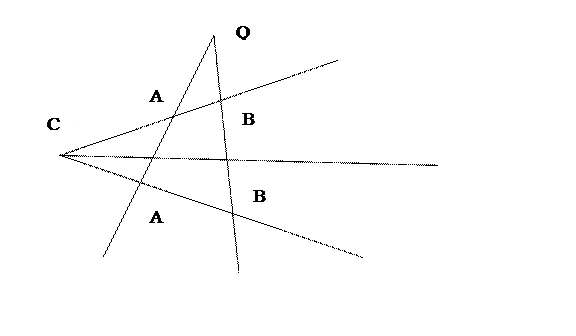
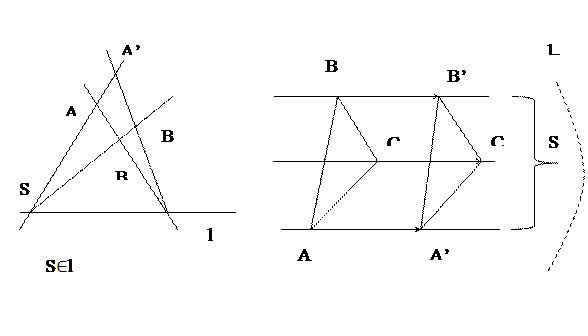
2) Центр и ось гомологии – собственные (S=Q, l=q).

Дано: Q не принадлежит q, A, A’, B не принадлежат Q.

Построить: B’ – образ точки B при данной гомологии.

Постоение:

1. AB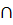q=c₀;

2. C₀A’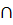QB=B’.

Построив точку C’, гомологичную точке С, не принадлежащей q, получим конфигурацию Дезарга.

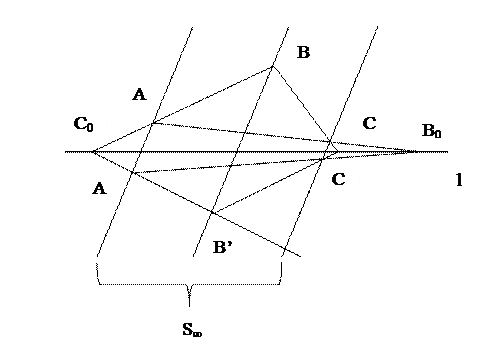
3) Центр – несобственная точка S_∞, ось – собственная прямая l, A и A’ – данные (гомологичные) точки.

Построение:

1. AB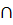l=C₀; AC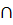l=B₀;

2. B’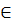A’C₀; BB’||AA’;

3. C’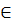A’B₀; CC’||AA’.

Родственное или перстпективно-аффинное преобразование (сжатие или растяжение к оси l).

4) Центр и ось – S=S_∞, l=l_∞, S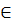_∞l_∞.

Параллельный перенос .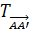

Выше рассмотренные случаи 1) - 3) дают примеры неособенной или гиперболической гомологии (центр S не лежит на оси l).

Если же центр гомологии S лежит на ее оси l, то гомология называется особенной или параболической.

Замечание 2: справедлива теорема: «всякое проективное преобразование является композицией некоторой гомологии и некоторого движения».