Определение 1. Проективной системой координат или проективным репером на проективной плоскости Ф 2 называется упорядоченная совокупность четырёх точек 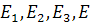 , никакие три из которых не лежат на одной прямой (точки общего положения). Точки
, никакие три из которых не лежат на одной прямой (точки общего положения). Точки 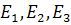 называются базисными, точка
называются базисными, точка 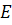 – единичной точкой. Прямые
– единичной точкой. Прямые 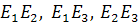 – координатные прямые.
– координатные прямые.
Обозначение: 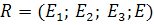 .
.
Определение 2. Проективными координатами точки M проективной плоскости Ф 2 в системе координат 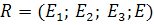 называются координаты
называются координаты 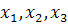 порождающего её вектора
порождающего её вектора 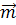 в базисе (
в базисе (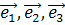 ), выбранном так, что:
), выбранном так, что:
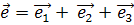
Замечание 1. Так как 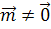 , то любая точка проективной плоскости имеет три проективные координаты, из которых хотя бы одна не равна нулю. Эти координаты задаются с точностью до числового множителя.
, то любая точка проективной плоскости имеет три проективные координаты, из которых хотя бы одна не равна нулю. Эти координаты задаются с точностью до числового множителя.
Обозначение: 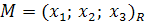 .
.
Пример 1. 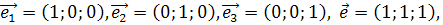 поэтому:
поэтому:
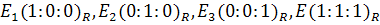
Замечание 2. Формула перехода от одной проективной системы координат 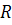 к другой
к другой 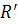 имеют вид:
имеют вид:
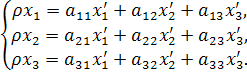
| (*) |
где 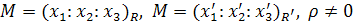 – произвольный числовой множитель, а
– произвольный числовой множитель, а
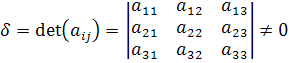
| (*) |
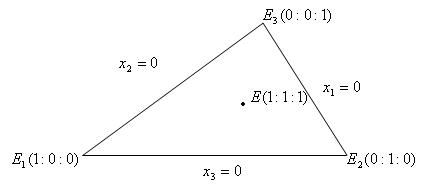
Определение 3. Проективная система координат 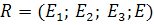 на расширенной евклидовой плоскости
на расширенной евклидовой плоскости 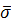 называется системой однородных координат, если две из её базисных точек являются несобственными.
называется системой однородных координат, если две из её базисных точек являются несобственными.
Обычно полагают 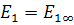 и
и 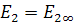 .
.
Пусть однородная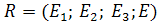 и неоднородная
и неоднородная 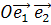 системы координат выбраны специальным образом (см. рисунок) на проективной плоскости Ф 2.
системы координат выбраны специальным образом (см. рисунок) на проективной плоскости Ф 2.
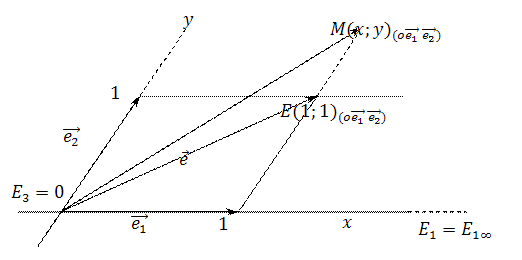
Тогда можно доказать теорему.
Теорема 1. Если:
1. Однородная 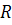 и неоднородная (
и неоднородная (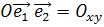 ) аффинные системы координат на расширенной евклидовой плоскости
) аффинные системы координат на расширенной евклидовой плоскости 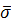 согласована указанным на рисунке способом.
согласована указанным на рисунке способом.
2. 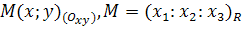 , где
, где 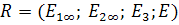 , то
, то
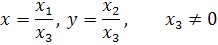
Замечание 3. Для собственных точек 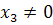 , для несобственных точек
, для несобственных точек 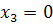 ; например,
; например, 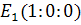 или
или 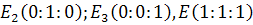 .
.
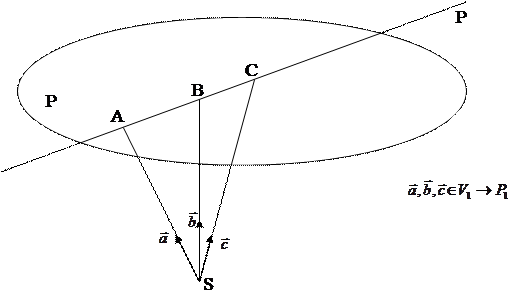
Теорема 2. Для того, чтобы три точки 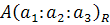 ,
, 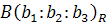 ,
, 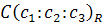 проективной плоскости Ф 2 лежали на одной проективной прямой Ф 1, где
проективной плоскости Ф 2 лежали на одной проективной прямой Ф 1, где 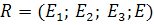 – проективная система координат, необходимо и достаточно, чтобы:
– проективная система координат, необходимо и достаточно, чтобы:
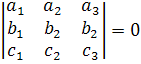
| (1) |
Доказательство:
Пусть точки 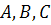 порождаются соответственно векторами
порождаются соответственно векторами 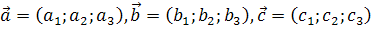 . Для того, чтобы эти точки лежали на одной проективной прямой Ф 1, необходимо и достаточно, чтобы векторы
. Для того, чтобы эти точки лежали на одной проективной прямой Ф 1, необходимо и достаточно, чтобы векторы 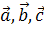 принадлежали векторному пространству
принадлежали векторному пространству 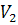 , порождающему проективную прямую Ф 1.
, порождающему проективную прямую Ф 1.
 Но тогда эти векторы линейно зависимы, следовательно, определитель (1) равен нулю, так как имеют линейно зависимые строки.
Но тогда эти векторы линейно зависимы, следовательно, определитель (1) равен нулю, так как имеют линейно зависимые строки.
Теорема 3. прямая P1, проходящая через две различные точки А(а1:а2:а3)R и В(в1:в2:в3)R проективной плоскости Р2 задается в системе проективных координат R=(Е1,Е2,Е3,Е) уравнением:
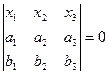 (2)
(2)
или
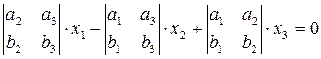 (3)
(3)
Доказательство:

 Согласно теореме 2 точка М(х1:х2:х3)R принадлежит прямой АВ в том и только в том случае, если имеет место равенство (2) или равносильное ему равенство (3).
Согласно теореме 2 точка М(х1:х2:х3)R принадлежит прямой АВ в том и только в том случае, если имеет место равенство (2) или равносильное ему равенство (3).
Следствие 1: координатные прямые Е1Е2, Е1Е3 и Е2Е3 имеют соответственно уравнения: х3=0, х2=0, х1=0.
Например, прямая Е1Е2:

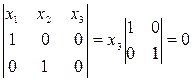
 .
.
Следствие 2: уравнение любой проективной прямой на проективной плоскости Р2 имеет вид:
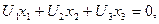
| (4) |
где коэффициенты (числа) 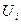 все равны нулю и определены с точностью до числового множителя.
все равны нулю и определены с точностью до числового множителя.
Доказательство:
 Положив в равенстве (3)
Положив в равенстве (3)
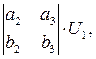
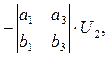
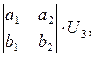
получаем уравнение (4). Так как точки A и B различны, то порождающие их векторы 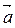 и
и 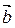 неколлинеарны, следовательно, их координаты не пропорциональны, и хотя бы один из определителей второго порядка отличен от нуля. Так как координаты точек A и B определены с точностью до общего числового множителя, то и числа
неколлинеарны, следовательно, их координаты не пропорциональны, и хотя бы один из определителей второго порядка отличен от нуля. Так как координаты точек A и B определены с точностью до общего числового множителя, то и числа 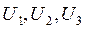 также определены с точностью до общего числового множителя.
также определены с точностью до общего числового множителя.
 Можно доказать, что и обратно, всякое уравнение вида (4) задает на проективной плоскости некоторую проективную прямую.
Можно доказать, что и обратно, всякое уравнение вида (4) задает на проективной плоскости некоторую проективную прямую.
Пусть 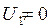 , тогда А (
, тогда А (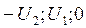 ) и В (
) и В (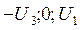 ) – точки, координаты которых удовлетворяют уравнению (4), подставив их в (2), получим уравнение (4).
) – точки, координаты которых удовлетворяют уравнению (4), подставив их в (2), получим уравнение (4).
Определение 4: коэффициенты 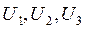 в уравнении (4) данной прямой
в уравнении (4) данной прямой 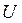 называются проективными координатами этой прямой.
называются проективными координатами этой прямой.
Обозначение: 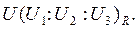
Пример 2. найдем координаты координатных прямых 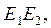
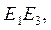
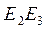 данного проективного репера R=(E1,E2,E3,E).
данного проективного репера R=(E1,E2,E3,E).
Согласно следствию 1 из теоремы 3 координатная прямая 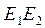 имеет уравнение х3=0 или
имеет уравнение х3=0 или 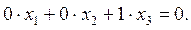 Тогда
Тогда 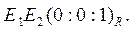
Аналогично получаем координаты двух других координатных прямых: 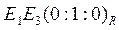 и
и 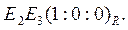
 2014-02-24
2014-02-24 5656
5656
