Отношения

Кроме рассмотренных выше элемен­тарных суждений для математического описания предпочтений в моделях при­нятия решений используется универ­сальное их представление в виде от­ношений.

Отношение — это математическое понятие для обозначения подмноже­ства прямого декартова произведения множеств.

Наиболее употребительными в прак­тике принятия решений являются би­нарные отношения, так как они хорошо связываются с традиционными спосо­бами выражения элементарных суж­дений.

Бинарным отношением R на мно­жестве элементов D называется под­множество упорядоченных пар (a", d") множества DXD всех таких пар.

Символом DXD обозначают прямое декартово произведение. Элементами множества D могут быть, например, исходы операции (в этом случае D = G). Если декартово произведение состоит более чем из двух «сомножи­телей» (DXDXD, DXDXDXD,...), то его элементами являются упорядо­ченные тройки, четверки элементов и т. д. В этом случае принципиально можно рассматривать тернарные, те-трарные и другие отношения.

Бинарные отношения могут быть использованы для универсального опи­сания связей между элементами раз­личной природы: для описания связ­ности электрических и информацион­ных сетей, иерархических структур управления и т. п.

Бинарные отношения есть множества специального вида, поэтому их опи­сание основывается на обычных спо­собах задания множеств: перечисле­нием элементов множества R, указа­нием общих свойств этих элементов, графом, матрицей смежности, подмно­жеством точек в декартовой системе координат.

Пример 2.3. Пусть R выражает мне­ние ЛПР о том, что частный показа­тель W_i не менее предпочтителен, чем показатель W_j, для векторного показателя W=(W₁, W₂, W₃, W₄), где W₁ — покупательная способность; W₂ — себестоимость; W₃ — затраты; W₄ — время на реализацию страте­гии. ЛПР, например, считает, что увеличение покупатель­ной способности не менее предпочти­тельнее снижения себестоимости и затрат, а снижение себестоимости, в свою очередь, не менее предпочти­тельнее снижения затрат (при усло­вии, что затраты не превышают допу­стимой нормы); фактор времени при этом не менее важнее снижения себе­стоимости и затрат. В этом случае от­ношение R можно записать: R = {(W_i, W_j)\(W₁, W₁), (W₁, W₂), (W₁ W₃,), (W₂, W₂), (W₂, W₃), (W_3, W₃), (W₄, W₂), (W₄, W₃) (W₄, W₄)} — как прямое перечисление показа­телей, связанных введенным отноше­нием; R= {(W_i, W_j)│W_i, W_j 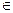W; W_i не менее предпочтительнее (важнее), чем W_j}— как указание общих свойств элементов.

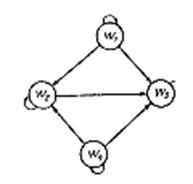
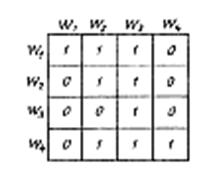
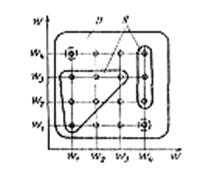
Это же отношение может быть пред­ставлено в виде графа, матрицы смеж­ности и множеством точек в декартовой системе координат (соответственно слу­чай а—в на рис. 2.1); направление стре­лок на рис. 2.1, а соответствует направ­лениям рассматриваемого предпочте­ния между элементами, которые они связывают. Петли на графе обозначают тот факт, что элемент не менее пред­почтителен самого себя.

С использованием указанных спо­собов графического представления от­ношений весьма удобно анализировать их свойства.

а	б	в

Рис. 2.1. Графическое представление бинарного отношения

«не менее предпочтителен (важен)»

Для формального опи­сания свойств бинарных отношений обозначим: (d!, d") 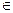R или d'Rd" — если элементы d', d" связаны отноше­нием R и (d', d") 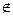R или d' "| Rd" — если элементы не связаны отноше­нием R.

Свойства бинарных отношений. Если для любого элемента d 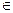D выпол­няется условие (d, d) 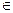R, то отноше­ние R рефлексивно (рис. 2.2, а).

Если для любой тройки элементов d, d', d" 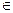D удовлетворяется условие, что из (d, d') 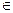R и (d¹, d") 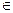R сле­дует, что (d, d") 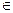R, то такое отно­шение называется транзитивным (рис.2.2, е).

Отношение R называется симметрич­ным, если из (d, d') 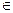R всегда сле­дует (d'_t d) 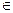R (рис. 2.2, б).

Отношение R называется связным (линейным, полным), если для любых двух несовпадающих элементов (d, d') 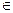D справедливо хотя бы одно из двух утверждений: либо (d, d') 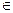R, либо (d', d) 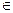R. Каждое из свойств бинарных отношений может иметь «антипода». Например, отношение мо­жет быть несвязным (рис. 2.2, д).

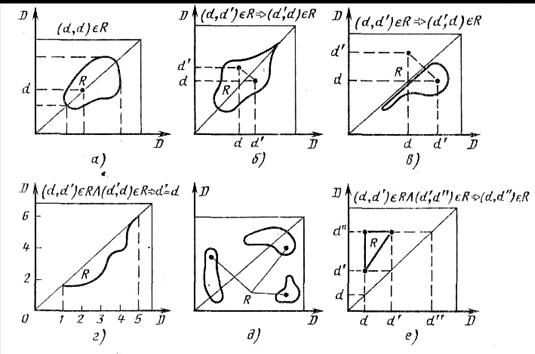
Рис. 2.2. Геометрическая интерпретация бинарного отношения

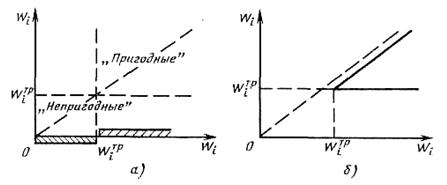
Рис. 2.3. Отношения эквивалентности и строгого частичного порядка

Если отношение R справедливо толь­ко для несовпадающих элементов из D, то оно называется антирефлексивным, то есть из (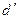, d") следует, что d' не есть d".

Если отношение R не является сим­метричным, то в зависимости от при­роды элементов d 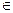D (числовые или нечисловые характеристики) вводятся свойства антисимметричности (для числовых) и асимметричности (для нечисловых).

Отношение R называется антисим­метричным, если из (d, d') 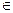R и (d', d) 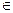R следует равенство d = d' (рис. 2.2, г).

Отношение R асимметрично, если из (d, d') 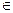R следует, что (d', d) 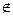R (рис. 2.2, в).

Дадим характеристику свойств би­нарного отношения на примере рис. 2.2. Введенное отношение рефлексивно. Признаком этого является наличие петель на графе, единиц — на диаго­нали матрицы смежности. Отношение R несвязно (отсутствует стрелка между W₁ и W₄ на графе), транзитивно.

Кроме того, отношение R асимме­трично (граф однонаправленный), область R в D на рис. 2.2, в геометрически несимметрична относительно диагонали.

Если бы отношение R рассматрива­лось только на элементах W₁,W₂, W₃, то оно обладало бы свойствами рефлексивности, транзитивности и связности.

В теории принятия решений особое место занимают отношения, обладаю­щие специальным набором указанных свойств. Это отношения эквивалент­ности, строго частичного порядка, квазипорядка и порядка.

Эквивалентностью называется сим­метричное, рефлексивное, транзитив­ное отношение. Это отношение имеет большое значение при формализации процессов и явлений (рис. 2.3, а). В ма­тематике оно связано с понятием раз­биения множеств на классы. Если отношение R есть эквивалентность на множестве D_j, то элементы d и d' относятся к одному классу Dj разбие­ний тогда и только тогда, когда (d, d') 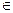R. И наоборот, если дано раз­биение D на классы {Dj}, то пара (d, а") 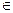Dj эквивалентна.

Строгим частичным порядком на­зывается антирефлексивное транзи­тивное отношение (рис. 2.3, б).

Квазипорядком называется рефлек­сивное и транзитивное отношение.

Порядком называется антисим­метричное рефлексивное транзитивное отношение.

В примере 2.3 множество всех значе­ний векторного показателя эффектив­ности W=(W₁, W₂, W₃, W₄)разби­вается на два класса: класс пригодных значений, для которого W₁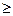20%; W₂ 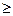5 %; W₃ 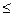20 000 р. и W₄ 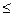t₀+ 12 месяцев (t₀ — момент вре­мени анализа альтернатив); класс не­пригодных значений, для которого не выполняется хотя бы одно из ука­занных условий.

В этом случае все альтернативы каждого класса эквивалентны, то есть в первом классе находятся все одина­ково пригодные, во втором — все одинаково непригодные. Отношение эквивалентности R задается указа­нием общего свойства: «быть пригод­ным». Использование дополнительной информации о предпочтении, например, «W_i не менее предпочтительнее (важ­нее) W_j»,позволяет на выделенном классе пригодных альтернатив по­строить квазипорядок, который в дан­ном случае оказывается несвязным (рис. 2.2). Если от ЛПР была бы получена информация типа: «W_i строго предпочтительнее W_j»и при этом она касалась бы любой пары аль­тернатив, то полученное на основе этой информации отношение было бы строгим частичным порядком, который обладает свойством антисимметрично­сти (значения показателей — действи­тельные числа). Для каждого из пока­зателей W_iотношения эквивалент­ности и строгого частичного порядка показаны на рис. 2.3.

Каждое из рассмотренных элементар­ных суждений (как способ выраже­ния предпочтений) может быть охарак­теризовано с помощью свойств би­нарных отношений.

Попарное сравнение в общем случае обладает только свойством рефлек­сивности. Поскольку сравнение эле­ментов проводится только в парах без учета остальных элементов, свой­ство транзитивности выявленного отношения предпочтения, как правило, отсутствует, а так как допускается указывать на несравнимость элемен­тов, то отсутствует и свойство связ­ности. Например, при попарном срав­нении ЛПР может указать, что уве­личение покупательной способности W₁предпочтительнее снижения себестои­мости W₂, а снижение себестоимости предпочтительнее снижения затрат W₃(при попарном сравнении последних). Из этого еще нельзя заключить, что W₁предпочтительнее W₃,так как при их попарном сравнении ЛПР может даже указать, что снижение затрат пред­почтительнее повышения покупатель­ной способности. Такой случай назы­вается нетранзитивностью в сужде­ниях ЛПР. Это обстоятельство является одним из главных недостатков одного из самых простых способов выражения элементарных суждений.

Сортировка может задавать либо отношение эквивалентности, либо толе­рантности (рефлексивное, симметрич­ное отношение) на предъявленном ЛПР множестве элементов. Так как среди предъявленных элементов ЛПР может уверенно отнести к тому или иному классу лишь элементы, субъ­ективно «сильно» различающиеся меж­ду собой, а среди оставшихся есть «похожие», то транзитивность на гра­ницах между классами может нару­шиться. В результате этого отноше­ние становится только рефлексивным и симметричным, что является оп­ределенным недостатком сортировки. Такое отношение называется толе­рантностью.

Ранжирование задает отношение квазипорядка. Если ранжирование строгое, то выявленное отношение является строгим частичным порядком.

Способы балльного оценивания субъ­ективных вероятностей и выражения предпочтения коэффициентами важ­ности устанавливают отношение по­рядка на предъявленном множестве элементов.

Наиболее серьезными недостатками части элементарных суждений яв­ляется отсутствие связности и тран­зитивности, что не позволяет осущест­вить однозначный выбор. В этом слу­чае необходимо либо привлечь до­полнительную информацию, раскры­вающую неопределенность и неодно­значность суждений ЛПР, либо ис­пользовать ряд непротиворечивых ги­потез для устранения указанных недо­статков. В качестве определяющей гипотезы при выработке решения выд­вигаются предположения о транзи­тивности и связности суждений ЛПР. Исходя из этой гипотезы, некоторое нетранзитивное отношение R можно аппроксимировать «ближайшим» к нему наименьшим транзитивным отноше­нием R, включающим в себя R. Та­кая операция называется транзитив­ным замыканием отношения R, ко­торое строится следующим образом:

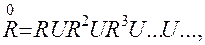
где R ² =R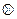R – композиция отношения R;

R³ =R²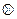R, R⁴ =R³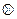R,…,

а композиция R² определяется по пра­вилу перемножения матриц смеж­ности отношений R с заменой арифме­тических операций операциями буле­вой алгебры.

Пример 2.4. Построим транзитивное замыкание для примера 1, когда при попарном сравнении установлено, что W₁ не менее предпочтительнее W₂, a W₂ не менее предпочтительнее W₃. Указанное отношение несвязно и нетранзитивно. Матрица смежности этого отношения выглядит следующим образом:

W₁ W₂ W₃

W₁ 1 1 0

R= W₂ 0 1 1

W₃ 0 0 1

Композиции отношения имеют вид

W₁ 1 1 1

R² = W₂ 0 1 1

W₃ 0 0 1

W₁ 1 1 1

R³ = W₂ 0 1 1

W₃ 0 0 1

Так как R³ совпадает с R², то ком­позиции более высокого порядка ис­кать не нужно. В этом случае тран­зитивное замыкание 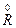совпадает с R², то есть появляется связь между элемен­тами W₁ и W₃.

Потеря транзитивности, как пра­вило, возникает в том случае, когда ЛПР не может четко выразить сужде­ние об отношении на множестве эле­ментов, что, например, при сортировке приводит к толерантности. В этом случае иногда применяют аппарат за­дания нечетких отношений предпочте­ний с использованием лингвистиче­ской переменной.