Теорема Котельникова

Данная теорема определяет условия, при которых непрерывный сигнал может быть восстановлен по своим отсчетам без потери информации.

Если имеется сигнал 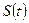, спектральная плотность которого не содержит составляющих с частотами выше 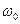, то:

1) он полностью определяется своими мгновенными значениями в дискретные моменты времени через интервал ;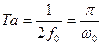

2) сигнал 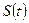может быть точно восстановлен по своим отсчетным значениям с помощью выражения:

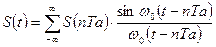. (14)

Выражение (14) может быть рассмотрено как ряд Фурье, базисные функции при этом 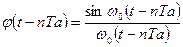сдвинуты относительно друг друга на .

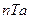Коэффициенты разложения при этом равны значениям восстанавливаемого сигнала в точках дискретизации.

Пример: На протяжении 10 сек. делаются выборки через 0.2 сек. Найти ДПФ.

Период дискретизации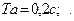

Частота дискретизации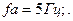

Суммарное время наблюдения .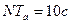

Период спектральной функции

.

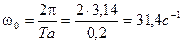Расстояние между двумя частотами:

.

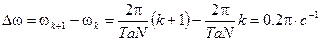В тригонометрической форме ДПФ имеет вид:

.

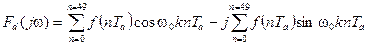Лекция №5. Функции окна. Виды окон.