Дискретный сигнал является последовательностью чисел, поэтому для анализа его представляют в виде дельта-функций с соответствующими множителями и задержками. Для последовательности отсчетов 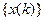 получится следующий сигнал:
получится следующий сигнал:
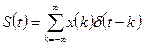 . (4)
. (4)
Преобразование Фурье линейно, спектр дельта-функции равен единице, а задержка сигнала во времени приводит к умножению спектра на комплексную экспоненту:
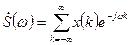 . (5)
. (5)
Из этой формулы видно главное свойство спектра любого дискретного сигнала: он является периодическим, и его период в этом случае равен 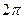 , т.е.
, т.е. 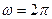 .
.
Рассмотрим несколько иную задачу. Пусть 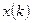 являются отсчетами аналогового сигнала
являются отсчетами аналогового сигнала 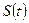 , взятыми с периодом
, взятыми с периодом 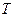 :
:
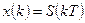 . (6)
. (6)
Выясним, как в этом случае спектр дискретного сигнала 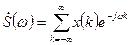 связан со спектром аналогового сигнала
связан со спектром аналогового сигнала 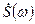 .
.
Итак, мы рассматриваем дискретизированный сигнал в виде последовательности дельта-функций, взвешенной значениями отсчетов 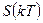 аналогового сигнала
аналогового сигнала 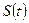 :
:
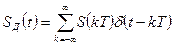 . (7)
. (7)
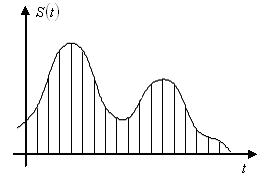
Рис 2. Дискретизированный сигнал в виде
последовательности дельта-функций.
Так как функция 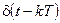 равна нулю всюду, кроме момента
равна нулю всюду, кроме момента 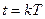 , то можно заменить в выражении (7) константы
, то можно заменить в выражении (7) константы 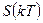 на исходный непрерывный сигнал
на исходный непрерывный сигнал
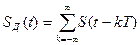 .
.
Как видно, сумма является периодическим сигналом, а поэтому может быть представлена в виде ряда Фурье. Коэффициенты этого ряда равны:
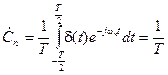 . (8)
. (8)
Таким образом, периодическая последовательность дельта-функций может быть представлена в виде комплексного ряда Фурье:
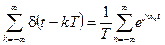 , (9)
, (9)
где 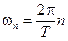 .
.
Сделав подстановку, получим:
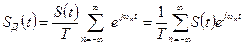 . (10)
. (10)
Умножение сигнала на 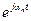 соответствует сдвигу спектральной функции на
соответствует сдвигу спектральной функции на 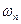 , поэтому спектр дискретизированного сигнала можно записать следующим образом:
, поэтому спектр дискретизированного сигнала можно записать следующим образом:
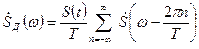 . (11)
. (11)
Таким образом, спектр дискретизированного сигнала представляет собой бесконечный ряд сдвинутых копий спектра исходного сигнала 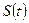 . Расстояние по частоте между соседними копиями спектра равно частоте дискретизации
. Расстояние по частоте между соседними копиями спектра равно частоте дискретизации 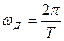 .
.
 2014-02-24
2014-02-24 2810
2810
