2014-02-24
631
Общая схема решения
Основной принцип решения задачи многокритериальной оптимизации с помощью теоретико-игрового подхода состоит в поиске компромиссного вектора X 0 в следующем виде:
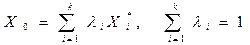, (2.2.1)
где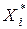 
– вектор, оптимальный для i -го критерия, l i – весовые коэффициенты.
Можно выделить следующую последовательность шагов решения задачи.
1. Решаем k задач линейного программирования (с помощью симплекс-метода), в которых имеется по одной функции цели и общая область ограничения. Таким образом, получаем k оптимальных векторов (для каждого критерия). Подробнее решение задач линейного программирования с помощью симплекс-метода рассмотрено в [2, 5].
Примечание. Если в системе ограничений имеются ораничения-равенства, то при решении задачи оптимизации с помощью симплекс-метода сначала требуется исключить все 0-строки.
2. Найдем меру неоптимальности каждого вектора X*i для остальных целевых функций:
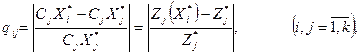(2.2.2)
где Cj ‑ вектор коэффициентов j-го критерия,
X*i – вектор, оптимальный для i-го критерия. Таким образом, qij – мера неоптимальности вектора 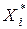для j -го критерия. Например, мера неоптимальности вектора 
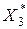для 2-го критерия
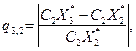
где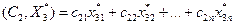 
,
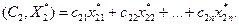
3. Сформируем квадратную матрицу, строки которой соответствуют k оптимальным векторам X*i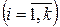 
, а столбцы ‑ k целевым функциям CjX ®ext 
.
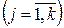| C 1 X | … | CkX | |||
| X* 1 | q 11 | … | q 1 k | ||
| … | … | … | … | (2.2.3) | |
| X*k | qk 1 | … | qkk |
Теперь сформулируем задачу в виде игровой. В качестве игрока P1 выберем совокупность оптимальных векторов X*i 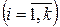, а в качестве игрока P2 – совокупность критериев оптимальности Zj 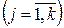. Тогда матрица (2.2.3) (с обратным знаком элементов) может рассматриваться как платежная матрица прямоугольной (матричной) игры двух партнеров X* и Z с нулевой суммой, которая определена множеством стратегий X* ={ X* 1, …, X*k } первого игрока и множеством стратегий Z ={ C 1 X, …, CkX } второго игрока. Элементы платежной матрицы должны иметь отрицательные знаки, так как они имеют смысл меры неоптимальности вектора, оптимального для какого-то из критериев, полученной при его подстановке в другой критерий, т.е. в игровой постановке – проигрыш первого игрока.
Тогда задача формулируется следующим образом: необходимо найти смешанную стратегию первого игрока, она и будет представлять искомые весовые коэффициенты l i для компромиссного вектора X 0.
Рассмотрим далее решение игровой задачи путем сведения ее к паре взаимно-двойственных задач линейного программирования.
При составлении платежной матрицы Q вычисляем ее элементы по формуле (2.2.2) и берем их с обратным знаком, при этом получим все диагональные элементы, равные нулю, т.е. матрица Q будет иметь вид
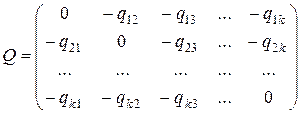(2.3.1)
В платежной матрице (2.3.1) все элементы, кроме диагональных, меньше нуля, что не позволяет использовать симплекс-метод для нахождения оптимального решения после сведения матричной игры к задаче линейного программирования. Поэтому предварительно матрицу Q (2.3.1) заменим эквивалентной ей матрицей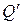 
с неотрицательными элементами, для чего к каждому элементу матрицы (2.3.1) прибавим одно и то же число, равное 
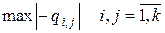, т.е. число, равное максимальному по модулю элементу матрицы (2.3.1). В результате получаем матрицу 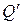с неотрицательными элементами:
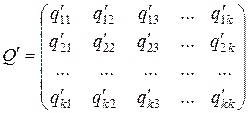, (2.3.2)
в которой диагональные элементы равны и имеют максимальное значение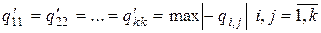 
и i ¹ j. Такая замена не изменит решения игры, изменится только ее цена (см. доказательство теоремы фон Неймана). Эквивалентная этой игре пара двойственных задач линейного программирования может быть представлена в совмещенной таблице вида
| v 1= | v 2= | … | vk = | W= | |||
- 
| - 
| … | - 
| ||||
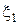
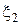
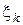
| u 1 |  =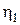
| 
| 
| … | 
| ||
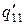
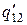
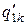
| u 2 |  =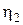
| 
| 
| … | 
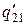
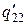
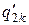
| (2.3.3) | |
| … | … | . | . | . | . | . | |
| uk |  =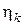
| 
| 
| … | 
| ||
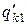
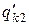
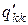
| Z = | -1 | -1 | … | -1 |
Решив с помощью симплекс-метода пару двойственных задач, представленных таблицей (2.3.3), получим max Z = min W, которые будут достигаться при каких-то определенных значениях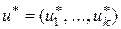 
. Оптимальную смешанную стратегию 
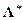первого игрока можно определить из полученных оптимальных решений данной пары двойственных задач по формуле
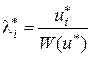. (2.3.4)
При этом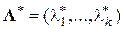 
удовлетворяет условию 
.
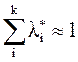Таким образом, искомый наилучший компромиссный вектор входных сигналов относительно заданных критериев оптимальности представляет собой выпуклую линейную комбинацию из оптимальных векторов входных параметров и имеет вид:
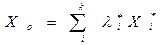. (2.3.5)
