Под полным исследованием функции понимается решение таких вопросов:
1.Определение области существования функции.
2.Выяснение вопроса о четности и нечетности функции.
3.Определение точек разрыва.
4.Определение асимптот графика функции.
5.Определение интервалов возрастания и убывания функции.
6.Определение экстремума функции.
7.Определение интервалов выпуклости и вогнутости.
8.Определение точек перегиба.
9.Определение точек пересечения графика функции с осями координат.
Полученные данные следует использовать для построения графика функции.
Задача. Исследовать средствами дифференциального исчисления функцию 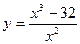 и построить ее график.
и построить ее график.
1.Функция определена и непрерывна на всей оси, кроме x=0. Здесь x=0- точка разрыва.
2.Функция ни четная, ни нечетная,т.к.
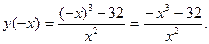
3.Найдем асимптоты графика функции:
а) вертикальная асимптота:
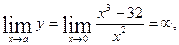 значит x=0 вертикальная асимптота.
значит x=0 вертикальная асимптота.
б) Наклонная асимптота 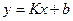 .
.
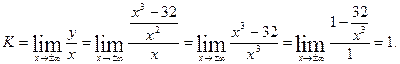
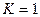 .
.
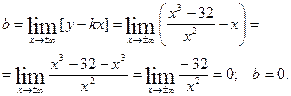
y=x- наклонная асимптота.
в) горизонтальная асимптота.
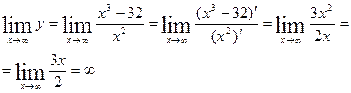 .
.
Горизонтальных асимптот нет.
4.Найдем интервалы возрастания и убывания функции. Найдем первую производную.
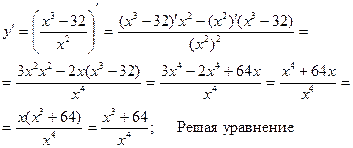
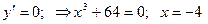 критическая точка.
критическая точка.
Исследуем знак 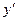 в интервалах.
в интервалах.
 |


 + - +
+ - +
В интервале 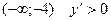 , функция возрастает.
, функция возрастает.
В интервале (-4;0) 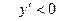 , функция убывает.
, функция убывает.
В интервале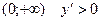 функция возрастает.
функция возрастает.
5.Определим экстремум функции: В точке х=-4 функция имеет максимум, т.к. 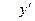 меняет знак с (+) на (-).
меняет знак с (+) на (-).
Найдем уmax.
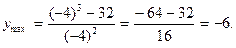
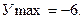 при
при 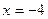
6.Определим интервалы выпуклости и вогнутости.
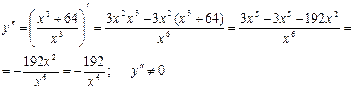
 |
- -
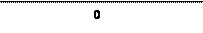 |
Определим знак второй производной в интервалах 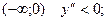
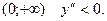
Значит функция в интервале 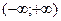 выпукла.
выпукла.
7.Нули функции:
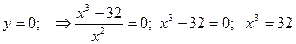 ;
; 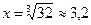
При х=3,2; у=0; х¹0; т.к. х=0 – точка разрыва функции.
Строим график функции.
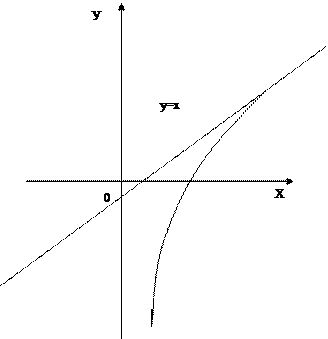
|

 2014-02-24
2014-02-24 547
547








