Таблица основных интегралов
Для облегчения интегрирования составляется таблица так называемых основных интегралов. Эта таблица получается из основных формул дифференциального исчисления. При этом целесообразно использовать те формулы дифференциального исчисления, в которых за аргумент принимается переменная u, являющаяся дифференцируемой функцией x. Справедливость каждой формулы проверяется дифференцированием.
1. 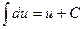 ; 2.
; 2. 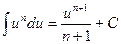 (при n≠1)
(при n≠1)
Проверка этой формулы:
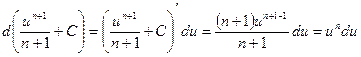
3. 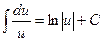 ; 4.
; 4. 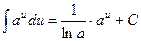
5. 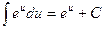 6.
6. 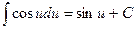
7. 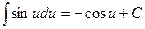 ; 8.
; 8. 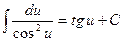
9. 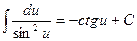 ; 10.
; 10. 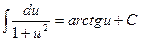
11. 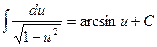 ; 12.
; 12. 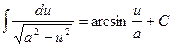
13. 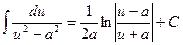 ;
;
14. 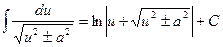 .
.
Вывод этих формул сводится к проверке того, что дифференциал правой части равен подынтегральному выражению в левой части равенства.
Интегрирование разложением есть приведение данного интеграла к сумме более простых интегралов.
Пример. Найти 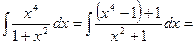
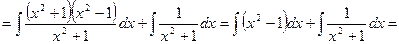
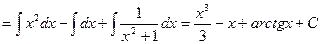
 2014-02-24
2014-02-24 955
955







