По этой формуле брус рассчитывается на прочность при изгибе

Для бруса прямоугольного сечения:

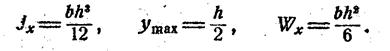
Для круглого сечения:

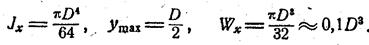
Т.о. при изгибе напряжения обратно пропорциональны третьей степени линейных размеров сечения. Наиболее экономичными являются такие формы поперечных сечений, для которых с наименьшей затратой материала получается наибольшая величина W _x. Чтобы форма сечения была рациональной, необходимо распределять площадь сечения подальше от нейтральной оси.

Так возникли стандартные прокатные профили - двутавр, швеллер, уголок и др.

При изгибе в вертикальной плоскости такие профили дают существенную выгоду по сравнению с прочими формами поперечных сечений. Моменты сопротивления стандартных профилей даются в соответствующих таблицах.

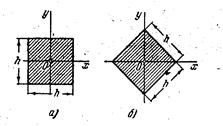
Пример 1. Как выгоднее расположить брус с квадратным сечением при изгибе по схеме а или б:

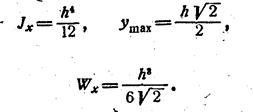
б)

Расположение а более выгодное: W_x^a=`1,4 W^b_x т.е. на 40% больше.

Пример 2. Подобрать двутавровое сечение балки, обеспечив двукратный запас прочности при F =20 Кн, а = 1м, σ_тр = 300 МПа.

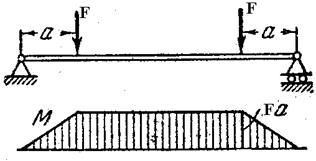
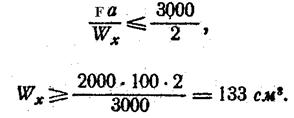
По таблице сортамента выбираем двутавр № 18, для которого W _x = 148 см³.

Недонапряжение 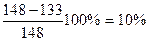- идет в запас прочности n=2,2.

Лекция 3. Поперечный изгиб. Напряжения при поперечном изгибе.

При поперечном изгибе в сечении бруса возникают не только М_изг, но и поперечная сила.

Следовательно возникают и σ и τ. Возникновение τ сопровождается появлением угловых деформаций γ.

τ распределены по сечению неравномерно, поэтому неравномерно будут распределены и угловые смещения т.е. поперечные сечения не остаются плоскими. Однако при Q = const искривление всех сечений происходит одинаково, т.е. сечения остаются плоскими. При Q переменной искривление весьма мало и имеет порядок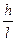, поэтому считают, что плоские сечения при поперечном изгибе, как и при плоском изгибе не искривляются.

Второй особенностью поперечного изгиба является наличие нормальных напряжений в продольных сечениях бруса – напряжения надавливания между слоями. Эти напряжения возникают только при Q переменной и имеют весьма малую величину, поэтому в пределах принятых допущений формулы для определения σ при чистом изгибе остаются справедливыми и при поперечном изгибе.

Касательные напряжения в поперечных сечениях бруса будут возникать от действия Q. Согласно закона парности они будут возникать и в продольных сечениях бруса.

Формула для их определения выводится из рассмотрения равновесия продольного сечения элемента бруса длиной dz и имеет вид:

τ = 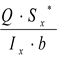- формула Журавского, где

Q – поперечная сила,

S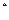_x – статический момент части продольного сечения, лежащая выше рассматриваемого слоя волокон,

I_x - момент инерции всего сечения,

b – ширина сечения.

Напряжения в поперечных сечениях равны им, как парные.

Пример: Определить закон изменения τ для прямоугольного сечения: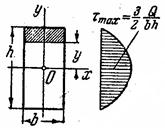

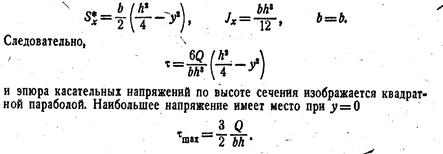
В связи с малостью величины τ _max расчет на прочность при поперечном изгибе производится только по σ, как и при чистом изгибе.

Дифференциальное уравнение изогнутой оси бруса и его интегрирование.

.

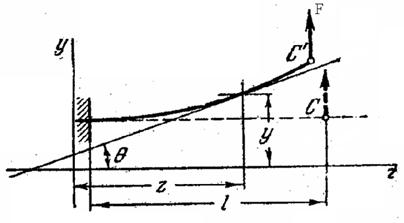
Форму изогнутой оси бруса или форму упругой линии можно определить из выражения кривизны (3), полученной при рассмотрении чистого изгиба.

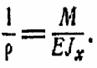
С другой стороны кривизна кривой в неподвижной системе координат yz определяется выражением (см курс аналитической геометрии):

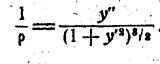
При рассмотрении малых перемещений tg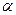 весьма мал. Поэтому будет мало и (y^’)² по сравнению с единицей и выражение кривизны можно записать в виде:

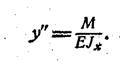
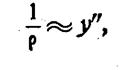или

Сопоставляя это с дифференциальными зависимостями между M, Q и q при изгибе (1) получим ряд соотношений:

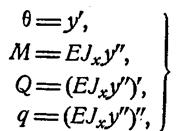При EI_x=const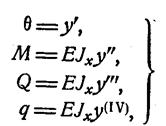

Из формул видно, что в случае нагружения бруса постоянного сечения

и равномерно распределенной нагрузкой получим: y ^IV =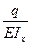= const,

т.е. форма оси изогнутого бруса описывается кривой четвертого порядка.

Если q =0 (Q=const),ось бруса изогнута по кривой третьего порядка.

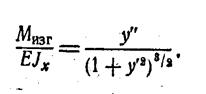Если решается задача при больших упругих перемещениях, то уравнение упругой линии будет иметь вид:

Стержни, получающие большие упругие перемещения, называются тонкими гибкими стержнями. Они имеют малую толщину и форму тонкой ленты или тонкой проволоки.

Общие методы изучения больших перемещений бруса при изгибе объединяются теорией гибких стержней.

Рассмотрим 2 примера определения формы упругой линии изогнутого бруса в области малых перемещений.

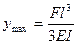
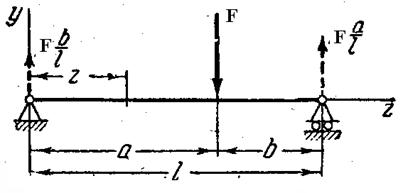
Пример 2.

Задача решается по аналогии с первой, но постоянных интегрирования при двух участках будет уже четыре.

Эта задача предлагается для самостоятельного решения.

Лекция 4. Метод начальных параметров. Универсальное уравнение упругой линии балки.

Из примеров видно, что если балка имеет п участков, необходимо совместно решить 2 п уравнений для определения 2 п постоянных интегрирования.

При большом числе участков это затруднительно.

Указанных затруднений легко избежать, если при составлении уравнения упругой линии придерживаться определенных правил.

Рассмотрим балку, нагруженную наиболее часто встречающимися силовыми факторами. Система сил взаимно уравновешена и на схеме указаны положительные их направления.

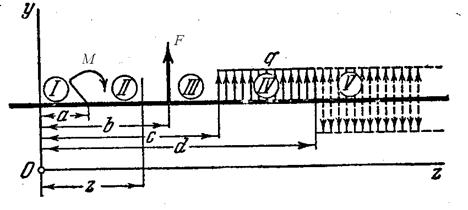
Задача заключается в выявлении особенностей, вносимых в уравнение упругой линии различными типами внешних силовых факторов. Запишем выражение М_изг для каждого участка: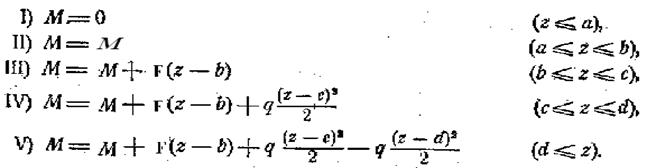

Выражение изгибающего момента для каждого последующего участка целиком включает в себя выражение предыдущего участка и отличается добавкой нового слагаемого. При переходе от четвертого к пятому участку указанная закономерность сохранена специально. Для этого нагрузка q продолжена на пятый участок (до конца балки) и добавлена отрицательная нагрузка q.

Имея ввиду, что М = EI_x y^’’, проинтегрируем, полученные выражения один раз не раскрывая скобок. Для сохранения однотипности полученных выражений, интеграл от Мнапишем в виде М(z-a), что скажется только на величине произвольной постоянной C_i.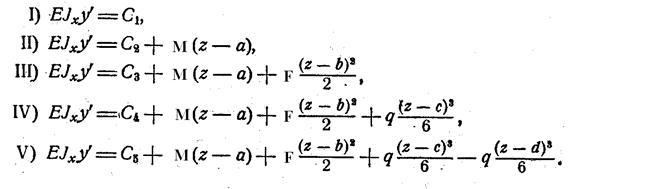

Постоянные С_i должны быть подобраны так, чтобы при переходе от одного участка к другому величина y^’ не терпела разрыва.

Т.е. при z=a, y₁^’=y₂^’; при z=b, y₂^’=y₃^’ и т.д. Поэтому С₁=С₂=С₃=С₄=С₅.

Из выражения для первого участка при z=0, y^’=y₀^’=θ₀ или EI_xθ₀ = C₁.

Подставляя C_i и интегрируя второй раз найдем:

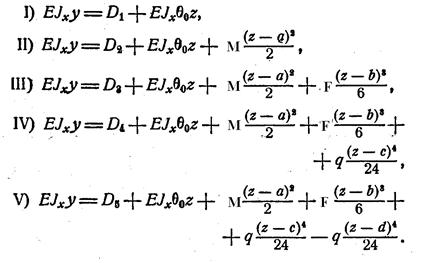
Постоянные D_i определяются из условий неразрывности функции y на границе участков. Поэтому D₁=D₂=D₃=D₄=D₅=EI_xy₀, y₀ – ордината упругой линии в начале координат.

Эти уравнения удобно записать в виде одного универсального уравнения упругой линии балки: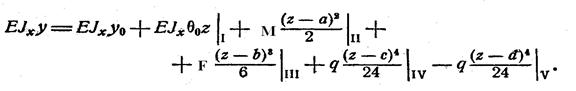

Для определения координат точек упругой линии каждого участка следует пользоваться членами уравнения, расположенными слева от вертикальной линии с индексом, соответствующего участка.

Пользуясь универсальным уравнением независимо от числа участков, необходимо определять только две постоянные y₀ и θ₀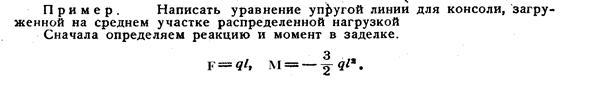

Лекция 5. Косой изгиб.

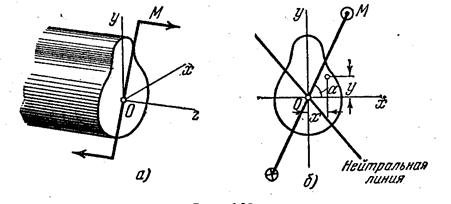Косым изгибом называется такой случай изгиба, при котором плоскость изгибающего момента не совпадает с главной осью сечения. Этот случай изгиба можно рассматривать как одновременный изгиб бруса в двух главных плоскостях.Раскладывая М на составляющие по x и y получим:

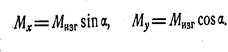Тогда уравнение нейтральной линии будет при σ = 0, или

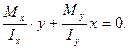
Обозначим k₁ = tgα, k₂ =-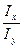ctgα, где k₁ – след плоскости момента,

k₂ – угловой коэффициент нейтральной линии.

Т.к. в общем случае I_x ≠ I_y, то условие перпендикулярности прямых не соблюдается, поскольку k₁ ≠ -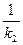, т.е. брус будет изгибаться не в плоскости М, а в некоторой другой плоскости, где жесткость на изгиб будет меньше. Поэтому нейтральная линия не перпендикулярна к плоскости М, а повернута в сторону оси минимального момента инерции.

Т.к. эпюра σ в сечении линейна, то σ _max возникает в точке, наиболее удаленной от нейтральной линии. Пусть координаты этой точки будут x₁ y₁.

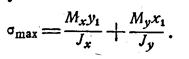
Тогда

Для сложного сечения x₁ y₁ определяются из чертежа графически.

Одновременное действие изгиба и продольной силы.

Если колонна имеет большую жесткость, то можно не учитывать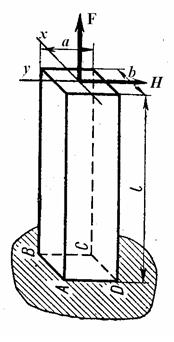 изгибающие моменты от деформации колонны.

В этом случае напряжение в произвольной точке будет:

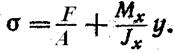
Если нагрузка Н вызывает моменты относительно обоих главных осей сечения, то

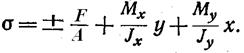
Для определения положения нулевой линии нужно составить ее уравнение

σ = 0. Максимальные напряжения, как и при косом изгибе будут в наиболее

удаленных точках сечения.

Внецентренное растяжение и сжатие.

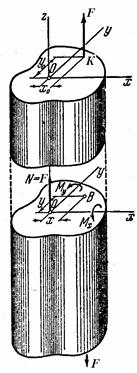При внецентренном растяжении равнодействующая внешних сил не совпадает с осью бруса, как при обычном растяжении, а смещена относительно продольной оси и остается ей параллельна.

Пусть К(x₀ y₀) точка приложения F. Тогда относительно осей x,y она дает моменты

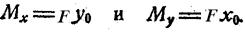
т.о. внецентренное растяжение – сжатие оказывается родственным косому изгибу, но в сечении кроме М_x М _y действует еще N = F.

В произвольной точке В(x,y):