Опр Ряд по степеням 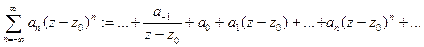 называется сходящимся на множестве
называется сходящимся на множестве 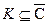 , если
, если 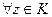 сходятся ряды
сходятся ряды 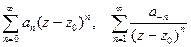 . В противном случае ряд называется расходящимся.
. В противном случае ряд называется расходящимся.
ТЕОРЕМА 10.5 (свойства функциональных рядов)
1) Если существует 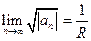 или
или 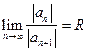 , то степенной ряд
, то степенной ряд 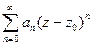 равномерно сходится внутри круга
равномерно сходится внутри круга 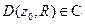 и расходится в каждой точке вне его замыкания
и расходится в каждой точке вне его замыкания 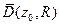 ; круг
; круг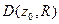 называется кругом сходимости, а число
называется кругом сходимости, а число 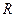 - радиусом сходимости степенного ряда. Сумма степенного ряда является аналитической функцией в круге сходимости.
- радиусом сходимости степенного ряда. Сумма степенного ряда является аналитической функцией в круге сходимости.
2) Пусть функция 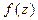 голоморфна на окружности
голоморфна на окружности 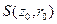 . Положим
. Положим
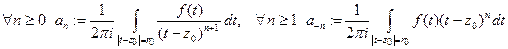 .
.
Пусть существуют пределы 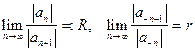 . Тогда ряд по степеням
. Тогда ряд по степеням 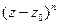 (ряд
(ряд
Лорана функции 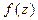 )
) 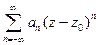 сходится к
сходится к 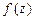 равномерно внутри кольца
равномерно внутри кольца
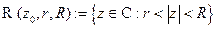 , и имеет на каждой компоненте его границы особые точки.
, и имеет на каждой компоненте его границы особые точки.
Пр 1 Целая функция 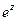 разлагается в ряд Маклорена
разлагается в ряд Маклорена 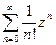 во всей комплексной плоскости.
во всей комплексной плоскости.
Пр 2 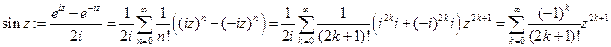 .
.
_____
Опр Особая точка 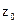 аналитической функции
аналитической функции 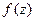 называется изолированной особой точкой однозначного характера (ИОТОХ), если
называется изолированной особой точкой однозначного характера (ИОТОХ), если 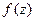 аналитична в некоторой проколотой окрестности
аналитична в некоторой проколотой окрестности 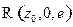 .
.
Опр ИОТОХ 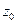 называется полюсом функции
называется полюсом функции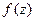 , если
, если 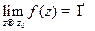 . Полюс
. Полюс 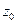 называется полюсом порядка
называется полюсом порядка 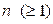 , если существует конечный и не равный нулю предел
, если существует конечный и не равный нулю предел 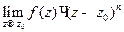 . Полюс первого порядка называется простым.
. Полюс первого порядка называется простым.
Пр Функция 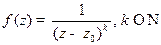 , имеет полюс порядка
, имеет полюс порядка 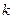 в точке
в точке 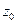 .
.
ЗАМЕЧАНИЕ Пусть функция 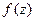 имеет ИОТОХ в
имеет ИОТОХ в 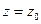 .
. 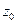 является полюсом тогда и только тогда, когда главная часть ряда Лорана имеет конечное число членов.
является полюсом тогда и только тогда, когда главная часть ряда Лорана имеет конечное число членов.
_____
Опр Пусть 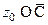 - ИОТОХ функции
- ИОТОХ функции 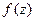 . Вычетом этой функции в точке
. Вычетом этой функции в точке 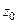 называется число
называется число 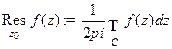 , где
, где 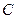 - замкнутая спрямляемая жорданова кривая, охватывающая
- замкнутая спрямляемая жорданова кривая, охватывающая 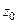 , причем ее внутренность
, причем ее внутренность 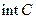 должна оставаться слева при обходе точки
должна оставаться слева при обходе точки 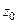 по контуру
по контуру 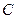 .
.
ЗАМЕЧАНИЕ В силу теоремы Коши 10.4.2вычет не зависит от выбора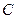 .
.
Опр Пусть КЗФ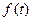 непрерывна на
непрерывна на 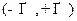 . Если существует конечный предел
. Если существует конечный предел
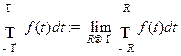 , то он называется интегралом в смысле главного значении.
, то он называется интегралом в смысле главного значении.
ТЕОРЕМА 10.6 (свойства вычетов)
1) Если 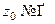 , то
, то 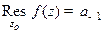 . Если
. Если 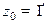 , то
, то 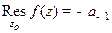 .
.
2) (основная теорема о вычетах) Если 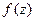 аналитическая в односвязной области
аналитическая в односвязной области 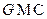 за исключением ИОТОХов
за исключением ИОТОХов 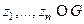 ,
, 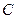 - спрямляемая замкнутая жорданова кривая в
- спрямляемая замкнутая жорданова кривая в 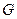 , охватывающая
, охватывающая 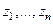 , то
, то 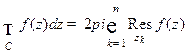 .
.
3) Пусть у рациональной функции 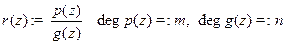 и
и 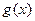 не имеет нулей на прямой
не имеет нулей на прямой 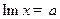 . Тогда
. Тогда
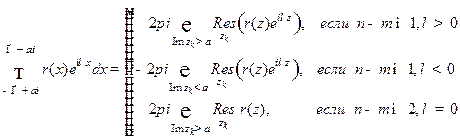 ,
,
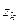 - нули
- нули 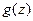 , лежащие в соответствующей полуплоскости.
, лежащие в соответствующей полуплоскости.
4) Если 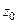 - полюс порядка
- полюс порядка 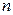 функции
функции 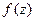 , то
, то 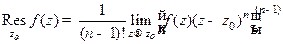 .
.
5) Пусть 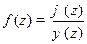 в окрестности
в окрестности 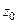 , функции
, функции 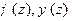 аналитична в
аналитична в 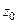 ,
, 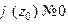 и
и
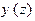 имеет простой нуль в точке
имеет простой нуль в точке 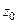 . Тогда точка
. Тогда точка 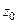 является простым полюсом функции
является простым полюсом функции 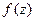 и
и 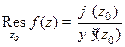 .
.
Пр 1 Вычислим интеграл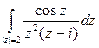 . Так как подынтегральная функция имеет простой полюс в точке
. Так как подынтегральная функция имеет простой полюс в точке 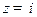 и полюс второго порядка в точке
и полюс второго порядка в точке 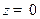 внутри контура интегрирования, то по основной теореме о вычетах и пунктам 4, 5 теоремы имеем
внутри контура интегрирования, то по основной теореме о вычетах и пунктам 4, 5 теоремы имеем
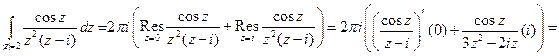
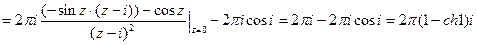 .
.
Пр 2 Вычислим интеграл 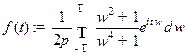 , который является обратным
, который является обратным
преобразованием Фурье функции 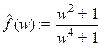 (смотри §8.3). При
(смотри §8.3). При 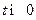 по пункту 3
по пункту 3
теоремы имеем
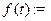
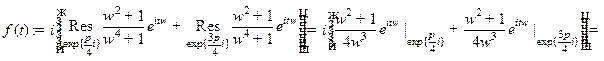
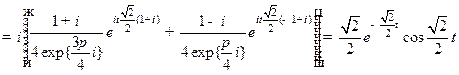 .
.
При 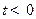
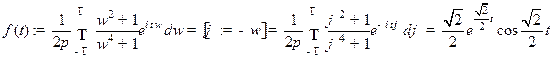 .
.
В целом, 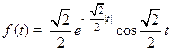 .
.
 2014-02-24
2014-02-24 1029
1029








