Интегрирование аналитических функций

Определение (Коши, 1825) Пусть 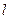есть кусочно гладкая кривая в област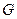и , и 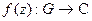- непрерывная функция комплексного переменного. Разобьем кривую точками 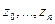, выберем точки 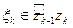. Образуем интегральную сумму 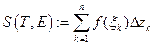,где 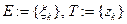. Обозначим 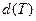диаметр разбиения кривой 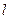. Интегралом от ФКП 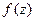на кривой l называется конечный предел.

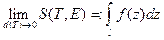ТЕОРЕМА 10.4 (свойства интеграла)

1) Если ФКП 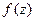непрерывна в односвязной области 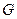, то равносильны утверждения:

а) 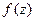голоморфна в 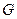; б) для любой спрямляемой кривой 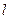интеграл 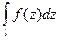зависит

только от ее концов; в) для любого замкнутого спрямляемого контура .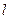

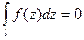2) (теорема Коши для сложного контура) Пусть граница 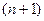-связной области 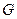состоит из внешне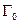й и 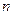штук внутренних 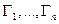кусочно гладких замкнутых жордановых кривых. Обход каждой из кривых выбран так, чтобы область 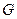оставалась слева. Если 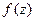аналитическая на 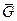, то .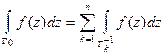

3) (формула Коши) Если 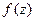аналитическая в точке 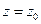, то

.

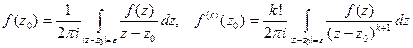Пр 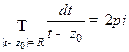. При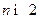

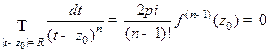
ЗАМЕЧАНИЕ (способы вычисления интегралов от ФКП)

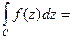
1)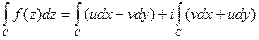, то есть с помощью КИВР.

2) Если 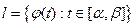- кусочно гладкая кривая, то 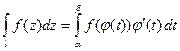, то есть с помощью интеграла от КЗФ.

3) Если 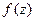голоморфна в односвязной област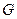и и 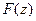- первообразная этой функции, то 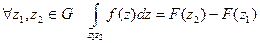, то есть с помощью формулы Ньютона-Лейбница.