ГЛАВА 16 ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
ГЛАВА 15 СЛУЧАЙНЫЕ ФУНКЦИИ
Опр Пусть дано вероятностное пространство 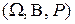 . Обозначим как и ранее
. Обозначим как и ранее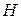 гильберто во пространство случайных величин на вероятностном пространстве
гильберто во пространство случайных величин на вероятностном пространстве 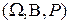 с нормой
с нормой 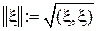 . Случайной функцией (СФ) называется отображение
. Случайной функцией (СФ) называется отображение 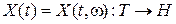 . Если
. Если 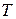 есть конечное или счетное множество:
есть конечное или счетное множество: 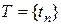 , то случайная функция называется случайной последовательностью и обозначает ся
, то случайная функция называется случайной последовательностью и обозначает ся 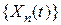 . Если
. Если 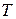 имеет мощность континуум, то
имеет мощность континуум, то 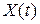 называется случайным процессом (СП). При этом для каждого фиксированного
называется случайным процессом (СП). При этом для каждого фиксированного 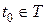 случайная величина
случайная величина 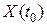 называется сечением случайного процесса, а для каждого фиксированного значения
называется сечением случайного процесса, а для каждого фиксированного значения 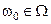 функция
функция 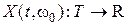 называется реализацией случайного процесса.
называется реализацией случайного процесса.
Пример 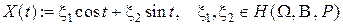 , есть случайный процесс.
, есть случайный процесс.
Опр Случайный процесс 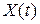 называется гауссовским, если каждая
называется гауссовским, если каждая 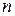 - мерная случайная величина
- мерная случайная величина 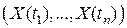 является
является 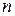 - мерной нормальной случайной величиной.
- мерной нормальной случайной величиной.
ЗАМЕЧАНИЕ Каждый гауссовский процесс однозначно определяется своим распределением вероятностей второго порядка и, следовательно, корреляционной функцией 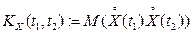 , где
, где 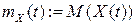 - математическое ожидание СП
- математическое ожидание СП
Опр Случайный процесс называется стационарным в широком смысле слова (ССП), если его матожидание не зависит от 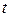 :
: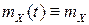 а
а 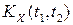 зависит от разности аргументов
зависит от разности аргументов 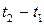 :
: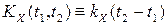
ЗАМЕЧАНИЕ Всюду ниже мы рассматриваем ССП, и для него корреляционной функцией будем называть 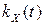 .
.
Пример Пусть в СП 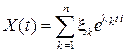 , где
, где 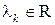 , а случайные величины
, а случайные величины 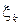 центри
центри
рованы и попарно не коррелированы. Тогда 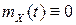 ,
, 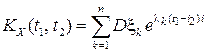 .
.
Опр Преобр. Фурье корреляционной функции ССП 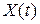
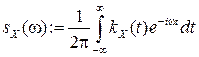 называется спектральной плотностью ССП.
называется спектральной плотностью ССП.
ТЕОРЕМА ( свойства спектральной плотности ССП)
1) Если 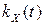 непрерывна, а
непрерывна, а 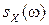 суммируема, то существует обратное преобразование Фурье
суммируема, то существует обратное преобразование Фурье 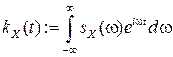 . В частности,
. В частности, 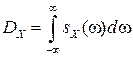 .
.
2) 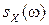 - четная функция. 3) Пусть стационарная линейная система управления описывается дифференциальным уравнением
- четная функция. 3) Пусть стационарная линейная система управления описывается дифференциальным уравнением 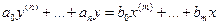 с передаточной функцией
с передаточной функцией 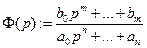 . Если эта система устойчива, и входной сигнал
. Если эта система устойчива, и входной сигнал 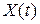 является ССП, то выходной сигнал
является ССП, то выходной сигнал 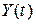 также является ССП и обладает свойствами: а)
также является ССП и обладает свойствами: а) 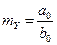 ,
,
б)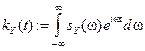 , где
, где 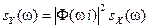 .
.
Обозначим 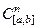 бесконечномерное пространство непрерывно дифференцируемых до
бесконечномерное пространство непрерывно дифференцируемых до 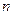 -го порядка включительно на отрезке
-го порядка включительно на отрезке 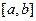 функций.
функций. 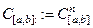 . Непосредственно по определению проверяется, что оно является нормированным в топологии, задаваемой нормой
. Непосредственно по определению проверяется, что оно является нормированным в топологии, задаваемой нормой 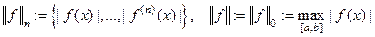 .
.
Элементы этого пространства иногда удобно называть точками.
ЗАМЕЧАНИЕ В соответствии с определением имеют место такие связи
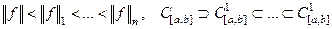 ,
,
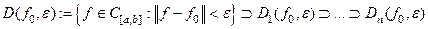 .
.
Опр Функционал 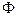 , определенный в некоторой окрестности точки
, определенный в некоторой окрестности точки 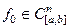 , называется непрерывным в точке
, называется непрерывным в точке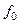 , если
, если 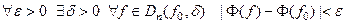 .
.
ЗАМЕЧАНИЕ 1 Линейный функционал 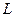 непрерывен в каждой точке
непрерывен в каждой точке 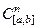 (то есть непрерывен на всем пространствеили просто непрерывен), если он непрерывен хотя бы в одной точке.
(то есть непрерывен на всем пространствеили просто непрерывен), если он непрерывен хотя бы в одной точке.
ЗАМЕЧАНИЕ 2 Линейный функционал 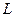 непрерывен тогда и только тогда, когда
непрерывен тогда и только тогда, когда 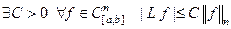 .
.
Опр Пусть функционал 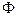 определен в
определен в 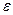 -окрестности точки
-окрестности точки 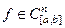 . Если его приращение
. Если его приращение 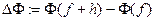 представимо в виде
представимо в виде 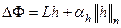 , где
, где 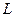 - линейный непрерывный функционал на
- линейный непрерывный функционал на 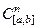 , а функционал
, а функционал 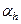 обладает свойством
обладает свойством 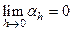 , то величина
, то величина 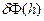 называется вариацией функционала
называется вариацией функционала 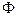 в точке
в точке 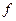 , а
, а 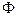 - дифференцируемым в точке
- дифференцируемым в точке 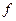 .
.
ЗАМЕЧАНИЕ 1 Пусть функционал 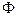 определен в некоторой окрестности точки
определен в некоторой окрестности точки 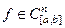 . Тогда
. Тогда 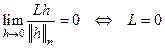 .
.
Фиксируем 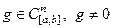 , и положим
, и положим 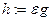 . Тогда
. Тогда 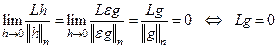
ЗАМЕЧАНИЕ 2 Имеет место равенство 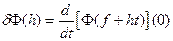 , то есть вариация функционала есть производная по направлению
, то есть вариация функционала есть производная по направлению 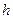 в точке
в точке 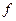 (производная Гато)
(производная Гато)
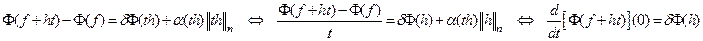 Опр Пусть функционал
Опр Пусть функционал 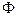 определен в окрестности точки
определен в окрестности точки 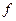 .
. 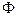 имеет слабый максимум в точке
имеет слабый максимум в точке 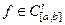 (сильныймаксимум в точке
(сильныймаксимум в точке 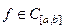 ), если
), если
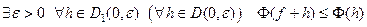 .
.
Аналогично определяется слабый минимум (сильный минимум).
ЗАМЕЧАНИЕ Точка сильного экстремума необходимо является и точкой слабого экстремума, так как 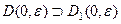 .
.
ТЕОРЕМА 16.1 Если функционал 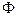 достигает экстремального значения в точке
достигает экстремального значения в точке 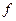 и дифференцируем в
и дифференцируем в 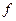 , то
, то 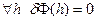 .
.
 2014-02-24
2014-02-24 753
753








