Литература
1. Подбельский В.В. Язык Cu ++: Учебное пособие. - М.: Финансы и статистика,1995, - 560 с.
2. Страуструп Б. Язык программирования Сг ++. - М.: Радио и связь, 1991. - 352 стр.
3. Собоцинский В.В. Практический курс Turbo Cu ++. Основы объктно- ориентированного программирования. - М.: Свет, 1993. - 236 с.
4. Романов В.Ю. Программирование на языке Cu ++. Практический подход. - М.: Компьтер, 1993. - 160 с.
5. Уинер Р. Язык турбо Cu. - М.: Мир, 1991. - 384 с.
6. Юлин В.А., Булатова И.Р. Приглашение к Cu. - Мн.: Высш. Шк., 1990,- 224 с.
7. Котлинская Г.П., Галиновский О.И. Программирование на языке Cu. -Мн.: Высш. Шк., 1991. - 156 с.
Опр ОДУ вида 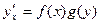 или вида
или вида 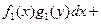
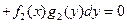 называется ОДУс разделяющимися переменными. ОДУ вида
называется ОДУс разделяющимися переменными. ОДУ вида 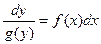 или вида
или вида 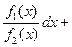
 называется ОДУс разделенными переменными.
называется ОДУс разделенными переменными.
ЗАМЕЧАНИЕ Решения этих уравнений выписываются в квадратурах:
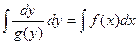 ,
, 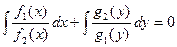 .
.
_____
Опр Функция 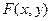 называется однородной функцией степени
называется однородной функцией степени 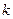 , если
, если
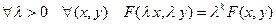 .
.
Пример 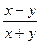 - однородная функция нулевой степени;
- однородная функция нулевой степени;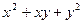 - однородная
- однородная
функция степени 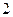 .
.
Опр ОДУ вида 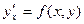 или вида
или вида 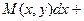
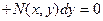 называется однородным, если соответственно
называется однородным, если соответственно 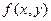 - однородная функция нулевой степени,
- однородная функция нулевой степени, 
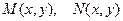 - однородные функции одинаковой степени.
- однородные функции одинаковой степени.
ЗАМЕЧАНИЕ Однородное ОДУ преобразуется в ОДУ с разделяющимися перемен ными, если зависимую переменную 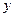 заменить на
заменить на 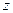 по формуле
по формуле 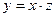 .
.
_____
Опр ОДУ вида 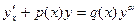 , где функции
, где функции 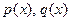 заданы и непрерывны, называется уравнением Бернулли, если
заданы и непрерывны, называется уравнением Бернулли, если 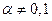 и линейным уравнением (ЛДУ) в противном случае.
и линейным уравнением (ЛДУ) в противном случае.
ЗАМЕЧАНИЕ Эти ОДУ решаются методом вариации произвольной постоянной. 1) Сначала решается ОДУ с разделяющимися переменными 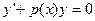 .
.
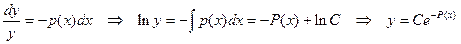 .
.
2) Решение исходного уравнения 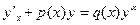 ищем в виде
ищем в виде 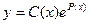 , считая в предыдущем решении произвольную постоянную зависящей от
, считая в предыдущем решении произвольную постоянную зависящей от 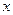 (говорят: варьируя произвольную постоянную
(говорят: варьируя произвольную постоянную 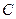 ). Для нахождения
). Для нахождения 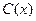 подставим это решение в
подставим это решение в
исходное уравнение: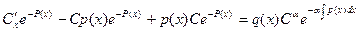 . После сокращения получаем уравнение с разделяющимися переменными для нахождения
. После сокращения получаем уравнение с разделяющимися переменными для нахождения 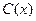 .
.
Пример Пусть в фильтре нижних частот входное напряжение изменяется по синусоидальному закону: 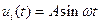 . Тогда уравнение фильтра нижних частот имеет вид
. Тогда уравнение фильтра нижних частот имеет вид 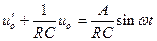 . Так как решение соответствующего однородного уравнения равно
. Так как решение соответствующего однородного уравнения равно 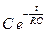 , то частное решение ищем в виде.
, то частное решение ищем в виде. 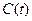 находим из уравнения с разделяющимися переменными
находим из уравнения с разделяющимися переменными 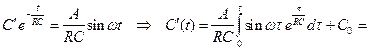
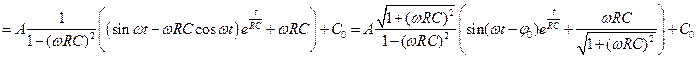 где
где 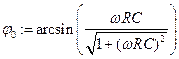 . Тогда падение напряжения на конденсаторе изменяется по закону
. Тогда падение напряжения на конденсаторе изменяется по закону 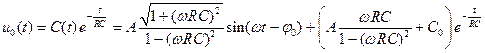 .
.
С течением времени второе слагаемое стремится к нулю. Поэтому 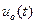 будет меняться периодически. Его амплитуда
будет меняться периодически. Его амплитуда 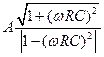 , очевидно, мала
, очевидно, мала 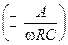 для больших (верхних) значений частот
для больших (верхних) значений частот 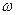 , что и объясняет название фильтра.
, что и объясняет название фильтра.
____
ЗАМЕЧАНИЕ 1 Решение ОДУ второго порядка вида 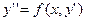 сводится к решению ОДУ первого порядка
сводится к решению ОДУ первого порядка 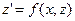 с помощью замены
с помощью замены 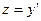 .
.
ЗАМЕЧАНИЕ 2 Решение ОДУ второго порядка вида 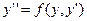 сводится к решению
сводится к решению
ОДУ первого порядка с помощью замены 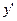 на зависимую переменную
на зависимую переменную 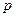 .
.
Первое очевидное. Докажем второе. 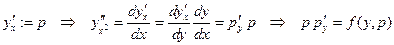 .
.
Пример (Уравнение колебаний математического маятника).
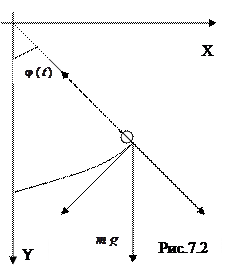 Материальная точка массы
Материальная точка массы 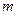 подвешена на нерастяжимой нити длины
подвешена на нерастяжимой нити длины 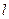 . На неё действуют две силы: вертикальная сила тяжести
. На неё действуют две силы: вертикальная сила тяжести 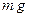 и сила реакции нити. Запишем закон колебаний маятника в виде
и сила реакции нити. Запишем закон колебаний маятника в виде
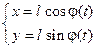 ,
,
где 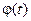 - угол его отклонения от положения равновесия в момент времени. Равнодействующая этих сил направлена по касательной к маятнику и потому второй закон Ньютона для него имеет вид
- угол его отклонения от положения равновесия в момент времени. Равнодействующая этих сил направлена по касательной к маятнику и потому второй закон Ньютона для него имеет вид
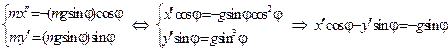 Продифференцируем первую систему два раза
Продифференцируем первую систему два раза
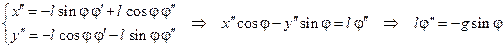 .
.
И мы вывели уравнение колебаний математического маятника 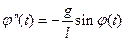
Это ОДУ второго порядка. Понизим его порядок с помощью замены
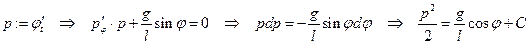 .
.
В крайнем левом положении 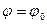 маятника по физическому смыслу имеем
маятника по физическому смыслу имеем
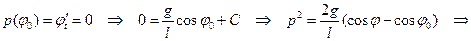
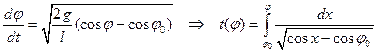 .
.
 2014-02-24
2014-02-24 442
442







