Опр Сеткой с шагом 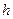 и узлами
и узлами 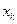 называется разбиение отрезка
называется разбиение отрезка 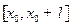 точками
точками 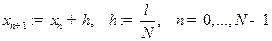 . Сеточной функцией называется функция, определенная в узлах
. Сеточной функцией называется функция, определенная в узлах 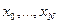 .
.
Пусть правая часть ОДУ 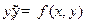 имеет непрерывные частные производные в точке
имеет непрерывные частные производные в точке 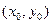 . Тогда по формуле Тейлора в окрестности точки
. Тогда по формуле Тейлора в окрестности точки 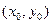 для решения
для решения 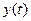 задача Коши:
задача Коши: 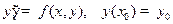 , имеем
, имеем
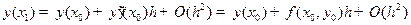 .
.
Последнее равенство подводит к такому определению.
Опр Методом Эйлера приближенного решения задачи Коши 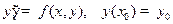 на сетке
на сетке 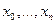 называется нахождение сеточной функции
называется нахождение сеточной функции 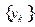 по формулам
по формулам
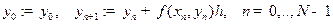 .
.
ЗАМЕЧАНИЕ Локальная погрешностьметода Эйлера – это погрешность на одном шаге, и она равна, как следует из формулы Тейлора, 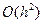 . Глобальная погрешность – это величина
. Глобальная погрешность – это величина 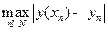 . Для метода Эйлера она равна
. Для метода Эйлера она равна 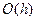 .
.
Опр Методом Рунге-Кутта приближенного решения задачи Коши 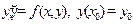 на сетке
на сетке 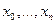 называется нахождение сеточной функции
называется нахождение сеточной функции 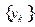 по формулам
по формулам
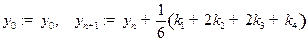 , где
, где 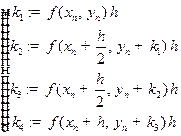 ,
, 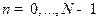 .
.
ЗАМЕЧАНИЕ 1 Локальная погрешность метода Рунге-Кутта на одном шаге равна 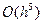 . Глобальная погрешность равна
. Глобальная погрешность равна 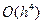 .
.
КПР Задачу Коши 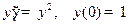 можно решить приближенно методом Рунге-Кутта на любом отрезке
можно решить приближенно методом Рунге-Кутта на любом отрезке 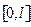 . Однако точное решение единственно и имеет вид
. Однако точное решение единственно и имеет вид 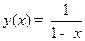 . Это видимое противоречие объясняется тем, что при определении глобальной оценки предполагается существование решения на всем отрезке, что в данном случае имеет место только на
. Это видимое противоречие объясняется тем, что при определении глобальной оценки предполагается существование решения на всем отрезке, что в данном случае имеет место только на 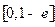 . Известны результаты, позволяющие определить характер точного решения по поведению приближенного.
. Известны результаты, позволяющие определить характер точного решения по поведению приближенного.
ЗАМЕЧАНИЕ 2 Методы Эйлера и Рунге-Кутта имеют место и для НСОДУ.
Пример Для задачи Коши 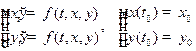 формула метода Рунге-Кутта имеет вид
формула метода Рунге-Кутта имеет вид 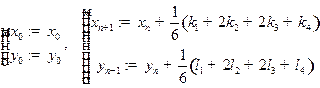 , где
, где
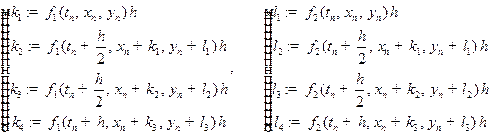 .
.
 2014-02-24
2014-02-24 411
411








