Движение точки под действием центральной силы, теорема площадей

Рассмотрим движение точки М массой m под действием силы 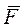, линия действия которой проходит через центр О во всё время движения точки М. Такую силу называют центральной.

Траектория материальной точки, движущейся под действием центральной силы, является плоской привой, лежащей в плоскости, проходящей через центр силы.

Согласно определению центральной силы, момент силы 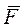относительно точки О

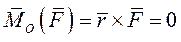
и из 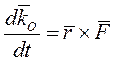следует, что

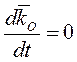или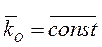

В проекциях:

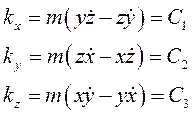
Умножая первое на x, второе на у, третье на z и складывая полученные выражения, получаем

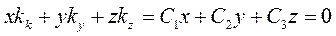
Т.е. координаты точки М(x,y,z) удовлетворяют уравнению плоскости, проходящей через начала координат.

Теорема площадей.

Запишем выражение для момента количества движения материальной точки 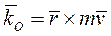, используя формулу 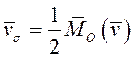для секторной скорости

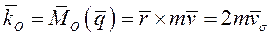
Преобразуем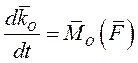

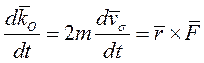
или

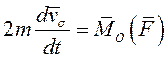
Записанную в таком виде теорему об изменении момента количества движения материальной точки называют теоремой площадей.