Если к абсолютно твердому телу приложена произвольная пространственная система сил, то изучение ее действия на это тело, в отличие от системы сходящихся сил, требует введения новых понятий. В частности, определения моментов силы относительно точки (центра) и оси. Понятия эти исторически появились в учении Архимеда о равновесии рычагов. Затем были обобщены для любых пространственных систем сил. В начале момент силы относительно точки рассматривался в плоскости, проходящей через линию действия и точку. Он определялся как произведение модуля силы на кратчайшее расстояние (плечо) от линии действия силы до точки, относительно которой брался момент. Причем эта величина считалась положительной, если сила, действующая на тело, стремилась вращать его против движения часовой стрелки и наоборот отрицательной, если она стремилась вращать тело по движению часовой стрелки. Однако при переходе к пространственным системам сил такое определение момента силы относительно точки стало недостаточным. Это в основном было связано с необходимостью учета возможных направлений плоскостей, проходящих через линии действия сил системы и общей для них моментной точки. В связи с этим, вводился такой вектор, приложенный в этой точке, числовое значение которого равно произведению силы на кратчайшее расстояние от моментной точки до линии действия силы и направленный перпендикулярно к той плоскости, в которой расположены линия действия силы и моментная точка. Причем здесь необходимо во внимание принимать и возможный поворот тела под действием силы вокруг выбранного центра. Теперь введем понятие момента силы сформулировав его следующим образом: моментом силы относительно какой-либо точки называется вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно к плоскости содержащей силу и выбранную точку, таким образом, чтобы с конца этого вектора можно было бы видеть стремление силы вращать тело против движения часовой стрелки.
|
|
|
Так как существуют правая и левая системы координат, то следует конкретно выбрать одну из них, чтобы единым образом определить направление векторного момента силы относительно точки. В дальнейшем будем пользоваться только первой системой координат. Это позволяет применить "правило буравчика", хорошо известное читателям еще со школьной скамьи.
Итак пусть даны сила  , приложенная в точке А какого-либо абсолютно твердого тела, и некоторый центр О (рис.2.11). Тогда моментом силы относительно точки О называется вектор, приложенный к центру (или точке) О, направленный перпендикулярно к плоскости треугольника ОАВ в ту сторону, откуда поворот тела, совершаемый силой, виден против хода стрелки часов (по правилу буравчика) и численно равный удвоенный площади треугольника ОАВ, иначе, этот вектор можно представить как векторное произведение радиуса-вектора
, приложенная в точке А какого-либо абсолютно твердого тела, и некоторый центр О (рис.2.11). Тогда моментом силы относительно точки О называется вектор, приложенный к центру (или точке) О, направленный перпендикулярно к плоскости треугольника ОАВ в ту сторону, откуда поворот тела, совершаемый силой, виден против хода стрелки часов (по правилу буравчика) и численно равный удвоенный площади треугольника ОАВ, иначе, этот вектор можно представить как векторное произведение радиуса-вектора 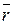 (т.е вектор, направленный от моментной точки О, к точке А приложения силы и модуль которого равен длине между этими точками) на силу, т.е.
(т.е вектор, направленный от моментной точки О, к точке А приложения силы и модуль которого равен длине между этими точками) на силу, т.е.
|
|
|
 =
= 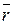 х
х  . (2.11)
. (2.11)
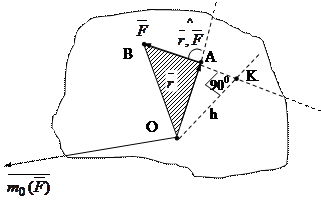 |
Рис.2.11.
Здесь для вектора момента силы введено обозначение  , где в индексе указывается точка, относительно которой берется момент, а внутри скобки сила, действующая на тело и сверху символа
, где в индексе указывается точка, относительно которой берется момент, а внутри скобки сила, действующая на тело и сверху символа  проводится прямая, означающая, что эта величина является векторной. Кроме этого обозначения в существующих литературах по теоретической механике применяются и такие обозначения
проводится прямая, означающая, что эта величина является векторной. Кроме этого обозначения в существующих литературах по теоретической механике применяются и такие обозначения 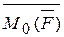 ,
, 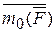 .
.
Теперь докажем, что модуль вектора  , представленного формулой (2.11) равен произведению величины силы на плечо, а направление векторного произведения двух векторов
, представленного формулой (2.11) равен произведению величины силы на плечо, а направление векторного произведения двух векторов 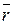 и
и  , т.е.
, т.е. 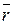 х
х  точно совпадает с направлением вектора
точно совпадает с направлением вектора  .
.
Как известно из векторной алгебры, модуль векторного произведения равен площади параллелограмма, построенного на векторах сомножителях 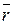 и
и  , т.е.
, т.е.
| 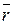 ×
×  |=rF×sin(
|=rF×sin(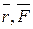 ).
).
Однако из прямоугольного треугольника KOA, где OK=h, имеем rsin(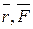 )=h. Следовательно, rFsin(
)=h. Следовательно, rFsin(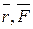 )=F×h=m0(
)=F×h=m0( ). Это выражение дает, что модуль вектора равен числовому значению вектора
). Это выражение дает, что модуль вектора равен числовому значению вектора  . Кроме того, вектор, равный векторному произведению
. Кроме того, вектор, равный векторному произведению 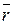 х
х  направлен по перпендикуляру к плоскости DAOB. Причем в ту сторону, откуда кратчайший поворот вектора
направлен по перпендикуляру к плоскости DAOB. Причем в ту сторону, откуда кратчайший поворот вектора 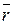 к направлению вектора
к направлению вектора  представляется происходящим против хода часовой стрелки, т.е. направление векторного произведения
представляется происходящим против хода часовой стрелки, т.е. направление векторного произведения 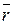 х
х  совпадает с направлением вектора
совпадает с направлением вектора  . Таким образом, формула (2.11) полностью определяет модуль и направление момента силы
. Таким образом, формула (2.11) полностью определяет модуль и направление момента силы  .
.
ЗАМЕЧАНИЯ
1.При переносе силы по линии ее действия в другие точки, допустим в М1, М2,…., Мn, ее момент  относительно данного центра не изменится (рис.2.12).
относительно данного центра не изменится (рис.2.12).
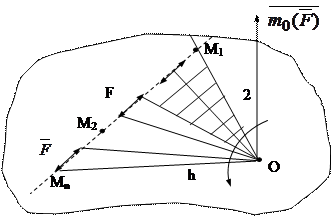 |
Рис.2.12.
То, что направления векторных произведений 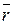 х
х  ,
, 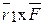 ,
, 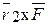 , …,
, …, 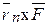 , перпендикулярных к одной и той же плоскости совпадают, а их числовые значения равны, не вызывают сомнений, так как равны площади соответствующих их параллелограммов, имеющих одно и то же основание
, перпендикулярных к одной и той же плоскости совпадают, а их числовые значения равны, не вызывают сомнений, так как равны площади соответствующих их параллелограммов, имеющих одно и то же основание  и одну и ту же высоту h.
и одну и ту же высоту h.
2.Момент силы  относительно центра О меняет свой знак при перестановке его сомножителей
относительно центра О меняет свой знак при перестановке его сомножителей 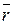 и
и  . Для доказательства этого составим векторное произведение
. Для доказательства этого составим векторное произведение  х
х 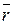 . Для этой цели откладываем от произвольной точки В вектор
. Для этой цели откладываем от произвольной точки В вектор  , а из конца его проводим вектор
, а из конца его проводим вектор 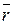 и на отложенных векторах строим параллелограмм (рис.2.13). Тогда направление вектора
и на отложенных векторах строим параллелограмм (рис.2.13). Тогда направление вектора  х
х 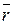 противоположно направлению
противоположно направлению 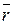 х
х  , а площади параллелограммов между собой равны. Таким образом,
, а площади параллелограммов между собой равны. Таким образом, 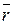 х
х  =-
=-  х
х 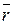 .
.
 |
Рис.2.13.
3.Момент силы относительно точки равен нуля, когда ее линия действия проходит через центр (точку) момента, так как в этом случае плечо равно нулю.
4.В случае, когда заданы величина и направление силы  и ее момент
и ее момент  относительно центра О, то всегда определима линия действия силы. При этом наикратчайшее расстояние h от моментной силы О до линии действия силы
относительно центра О, то всегда определима линия действия силы. При этом наикратчайшее расстояние h от моментной силы О до линии действия силы  , т.е. плечо h находится из выражения h=|
, т.е. плечо h находится из выражения h=|  | / F.
| / F.
Момент силы относительно точки О можно также определить, зная проекции силы на прямоугольные декартовы оси и координаты точки приложения силы х, y, z. Действительно, если иметь в виду выражение (2.11), то момент силы  относительно этих проекций выражается следующим образом:
относительно этих проекций выражается следующим образом:
 =
= 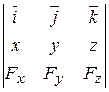 (2.12)
(2.12)
ЗАМЕЧАНИЕ
Если все силы, действующие на тело лежат в одной плоскости, то векторы, изображающие моменты этих сил относительно какой-либо точки, лежащей в той же плоскости, будут перпендикулярны к плоскости. Следовательно, в данном случае моменты сил различаются между собой только числовой величиной и знаком, а не направлением, как в случае пространственной системы сил и их можно рассматривать как скалярные величины. При это величина момента силы равна m0( )=|
)=|  | = ±F×h, где знак ± зависит от того, куда сила стремиться вращать тело (+ соответствует вращению тела против движения часовой стрелки и наоборот - движения часовой стрелки). Раскрывая определитель (2.12) по столбцам получим:
| = ±F×h, где знак ± зависит от того, куда сила стремиться вращать тело (+ соответствует вращению тела против движения часовой стрелки и наоборот - движения часовой стрелки). Раскрывая определитель (2.12) по столбцам получим:
|
|
|
 =(yFz-zFy)
=(yFz-zFy) 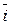 +(zFx-xFz)
+(zFx-xFz) 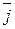 +(xFy-yFx)
+(xFy-yFx) 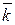 (2.13)
(2.13)
В то же время, если проекции этого момента силы на прямоугольные декартовы оси координат соответственно обозначим через m0х( ), m0y(
), m0y( ), m0z(
), m0z( ), то для m0(
), то для m0( ) находим:
) находим:
 =m0x(
=m0x( )
) 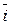 +m0y(
+m0y( )
) 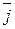 + m0z(
+ m0z( )
) 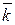 (2.14)
(2.14)
Далее сравнивая выражения (2.12) и (2.13), которые определяют одну и ту же величину, получим:
m0x( )=yFz-zFy, m0y(
)=yFz-zFy, m0y( )=zFx-xFz, m0z(
)=zFx-xFz, m0z( )=xFy-yFx (2.15)
)=xFy-yFx (2.15)
Формула (2.15) называется аналитическими выражениями моментов силы относительно координатных осей, что будет доказано ниже.
Момент силы относительно оси. Пусть к некоторому твердому телу в точке А приложена сила  . Чтобы вычислить момент этой силы относительно какой-либо оси (допустим ею является ось OZ), следует спроектировать силу
. Чтобы вычислить момент этой силы относительно какой-либо оси (допустим ею является ось OZ), следует спроектировать силу  на перпендикулярную плоскость Pz к указанной оси, затем взять момент от проекции
на перпендикулярную плоскость Pz к указанной оси, затем взять момент от проекции  относительно точки О1 пересечения оси с перпендикулярной плоскостью, взяв его со знаком плюс или минус (рис.2.14). Момент силы относительно оси обозначив символом mz(
относительно точки О1 пересечения оси с перпендикулярной плоскостью, взяв его со знаком плюс или минус (рис.2.14). Момент силы относительно оси обозначив символом mz( ), согласно выше сказанному, можно его записать следующим образом:
), согласно выше сказанному, можно его записать следующим образом:
mz( )=±Fn×H (2.16)
)=±Fn×H (2.16)
При этом момент силы относительно оси mz( ), вычисляемый соотношением (2.16) может быть взят со знаком плюс, если проекция
), вычисляемый соотношением (2.16) может быть взят со знаком плюс, если проекция 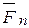 силы
силы  стремится вращать тело против движения часовой стрелки; когда смотрим с конца оси и со знаком минус в противном случае.
стремится вращать тело против движения часовой стрелки; когда смотрим с конца оси и со знаком минус в противном случае.
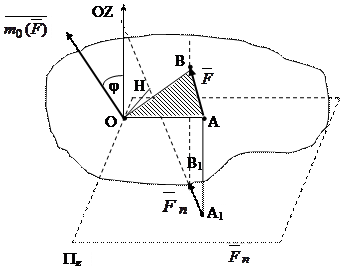 |
Рис.2.14.
ЗАМЕЧАНИЯ
1.Значение момента силы относительно оси может быть также выражено удвоенной площадью треугольника
mz( ) = 2
) = 2 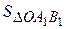 (2.17)
(2.17)
2.Если проекция 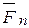 силы
силы  на перпендикулярную плоскость Pz к оси OZ относительно которой берется момент равна нулю, т.е Fn=0, то линия действия силы параллельна к этой оси.
на перпендикулярную плоскость Pz к оси OZ относительно которой берется момент равна нулю, т.е Fn=0, то линия действия силы параллельна к этой оси.
3.Если расстояние от точки О пересечения оси OZ с перпендикулярной плоскостью Pz до линии действия проекции 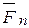 силы
силы  на эту плоскость равно нулю, т.е. H=0, то линия действия силы
на эту плоскость равно нулю, т.е. H=0, то линия действия силы  пересекает ось, относительно которой вычисляется момент.
пересекает ось, относительно которой вычисляется момент.
|
|
|
Таким образом, момент силы относительно некоторой оси равен моменту проекции силы на перпендикулярную плоскость к этой оси, взятому относительно точки пересечения оси с перпендикулярной плоскостью.
Также, можно показать, что проекция вектора момента силы относительно некоторой точки на ось, проходящую через эту точку, равна моменту силы относительно этой же оси. Для этого заметим, что проекция m0z( ) вектора момента
) вектора момента  на ось OZ равна
на ось OZ равна
m0z( )=прOZ[
)=прOZ[  ]=|
]=|  |cosj=2SDOABcosj=±2
|cosj=2SDOABcosj=±2 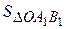 (2.18)
(2.18)
так как угол j между вектором  и осью OZ равен углу между плоскостями DOAB и Pz, где площадь DOA1B1 есть проекция площади DOAB. Однако по определению момент силы относительно оси определяется выражение вида (2.17). Далее, сравнивая (2.17) с (2.18), имеем, что
и осью OZ равен углу между плоскостями DOAB и Pz, где площадь DOA1B1 есть проекция площади DOAB. Однако по определению момент силы относительно оси определяется выражение вида (2.17). Далее, сравнивая (2.17) с (2.18), имеем, что
m0z( )=mz(
)=mz( ),
),
что и требовалось показать. Следовательно, чтобы вычислить моменты силы относительно соответствующих осей координат X,Y,Z можно использовать соотношения вида (2.15).
1. Что называется сходящейся системой сил?
2. Как определяется равнодействующая системы сходящихся сил геометрически и аналитический способами?
3. Сформулируйте и запишите условия равновесия системы сходящихся сил в векторной и аналитической формах.
4. Если для плоской системы сходящихся сил åFkx=0, а åFky¹0, что можно сказать о ее равнодействующей?
5. Может ли находиться в равновесии система 3-х сходящихся сил, не лежащих в одной плоскости?
6. Дайте определение векторного момента силы относительно центра. Где он приложен, как направлен?
7. Нарисуйте рисунок, изображающий векторное произведение. Запишите векторный момент силы относительно центра в виде векторного произведения радиуса-вектора точки приложения силы на вектор силы.
8. Как определяется модуль момента силы относительно центра? Что называется плечом силы? Как выражается момент силы относительно центра через площадь треугольника.
9. Дайте определение алгебраического момента силы относительно центра.
10. В каких случаях момент силы относительно центра равен нулю.
11. Дайте определение момента силы относительно оси. В каких случаях этот момент равен нулю.
12. Запишите формулы для моментов силы относительно координатных осей.
13. Какова связь между моментом силы относительно оси и векторным моментом силы относительно любой точки, лежащей на этой оси?
 2015-02-27
2015-02-27 5398
5398
