Решающие правила отображений

Однозначное отображение состояний измеряемых характеристик в область абстракции означает эквивалентность состояний величин. Создаваемый при этом образ действительности недостаточен, так как он не отражает те количественные отношения, в которых находятся образы состояний данной характеристики. Для достоверности отображения необходимо, чтобы отношения между состояниями а измеряемых характеристик были такими же, как и между значениями величин в области абстракции. Рассмотрим те отношения между значениями величин, которые имеют принципиальное значение, имея в виду что они аналогичны соотношениям между состояниями характеристик реальной области, т.е. изоморфны.

- Отношение эквивалентности состоит в том, что любые два элемента множества значений величин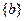состоят в одном из двух соотношений

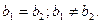
- Отношение строгого упорядочения состояний заключается в соответствии элементу множества 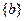определенного положения на числовой оси и выполнении одного из неравенств

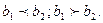
- Отношение эквивалентности и строгого упорядочения интервалов выполняется в том случае, когда для разности двух элементов множества 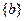относительно разности двух других элементов справедливо одно из неравенств

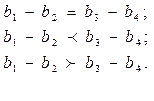
- Отношение эквивалентности и строгого упорядочения частных подразумевает, что каждое частное от деления двух элементов множества в отношении к частному от деления двух других элементов определяется одним из выражений

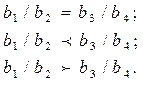
Вышеприведенные соотношения, положенные в основу создания образа действительности (в области абстракции), отражающего состояние характеристик объектов, справедливы только, когда значения величин отображения принадлежат множеству положительных действительных чисел.

1.4.Решающие правила отображения ЭСО в МСО

Для формирования измерительной шкалы из множества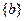необходимо выбрать только один элемент , который лучше всех отображает состояние а. Выбор такого

Рис.16. Математические методы, используемые в теории измерений

Рис. 17. Элементы эмпирической и математической систем отношений

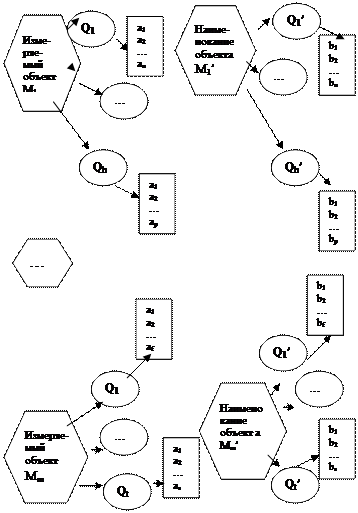
Рис.18.Отображение элементов реальной области в область абстракции

элемента выполняется в соответствии с решением D таким, что .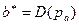

Для решения этой задачи используют решающие правила.

1. В соответствии с первым решающим правилом выбирают наиболее вероятное значение 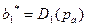такое, что 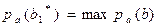, т.е. модальное значение.

2.В соответствии со вторым правилом выбирают среднее значение 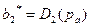такое, чт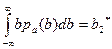о либо .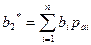

2.Третье правило предусматривает выбор в качестве отображающего элемента 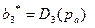медианы .

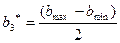Графическое изображение образов состояния а для правил решения D ₁, D ₂, D ₃ приведено на рис.19. При симметричной дифференциальной функции распределения вероятности значения 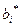могут быть одинаковы.