2014-02-24
748
Одной из наиболее практически значимых задач является построение плавных временных зависимостей функции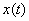 
, если эта функция имеет случайную составляющую. Дискретную зависимость 
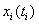называют временным рядом или, в общем случае, дискретным случайным процессом. Общие свойства и методы описания случайных процессов мы рассмотрим в пятой главе настоящего пособия. По сравнению с экспериментальными зависимостями 
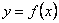, которые мы считали результатом однофакторного эксперимента и рассмотрели выше, особенности экспериментальных временных рядов заключаются в следующем:
1. На практике обычно приходится анализировать временные ряды с достаточно большим количеством отсчетов (не менее нескольких десятков).
2. Отсчеты, как правило, производятся через равные промежутки времени (равноотстоящие узлы зависимости при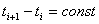 
)
3. Зависимость 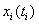заведомо немонотонна и, чаще всего, ограничена. Поэтому, если выбрать конечный интервал 
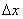, то для любого 
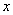с увеличением длины временного ряда количество значений 
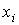, попадающих в интервал 
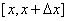будет увеличиваться.
|
|
|
4. Приближающую функцию, аппроксимирующую временной ряд по всей его длине, как правило, невозможно описать аналитически.
Особенности временных рядов хорошо поясняет простейший пример. Проведем однофакторный эксперимент, регистрируя значения входных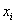 
и выходных 
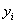параметров одновременно, в моменты времени 
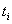, через равные промежутки 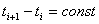. Тогда функциональная зависимость 
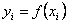, описывающая результаты эксперимента, задается параметрически, через два временных ряда , 
.
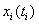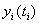В теории обработки временных рядов существует множество способов их сглаживания: фильтрация с использованием преобразования Фурье, кусочная аппроксимация многочленами и др… Мы рассмотрим два простейших, но принципиально разных вида сглаживания, которые, в какой-то мере, обобщают особенности этой процедуры:
1)метод скользящего среднего;
2)медианное сглаживание.
Рассмотрим две случайные зависимости, показанные на рис.3.7. Зависимости имеют одинаковую регулярную составляющую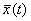 
, а случайные составляющие зависимостей отличаются: зависимость рис.3.7,б кроме мелких случайных флуктуаций имеет редкие выбросы достаточно большой амплитуды.
а б
Рис.3.8
Целью сглаживания является получение плавной зависимости 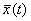. Метод скользящего среднего предполагает выбор окна усреднения 
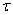, и для каждого 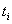рассчитывается среднее значения на этом интервале:
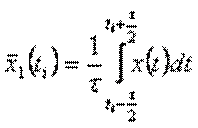. (3.3.1)
Этот метод позволяет сгладить случайную составляющую зависимости, то есть избавиться от высокочастотных флуктуаций. При этом фильтрация высоких частот зависит от длины интервала усреднения .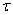
Если применить метод скользящего среднего к зависимости рис.3.7,б, имеющей значительные, но редкие выбросы, то полученная сглаженная зависимость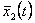 
резко отличается от 
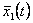. Выбросы, за счет их высокой амплитуды, сильно влияют на среднее значение, как только попадают в интервал усреднения, то есть каждый выброс искажает 
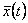на интервале длиной 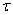. В случае, когда выбросы имеют редкий и случайный характер, для выделения регулярной составляющей метод скользящего среднего неприемлем.
|
|
|
При наличии редких выбросов (рис.3.7,б) удобнее применять метод медианного сглаживания, в котором на «скользящем» интервале 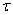для получения 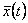используется не среднее значение функции, а медиана.
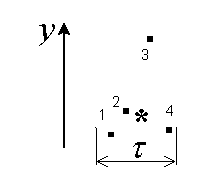
Рис.3.9
Пусть на интервал 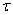попало четыре значения временного ряда 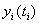, и одно из значений 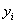сильно отличается от других (см. рис.3.9, точка 3). Построение медианы по 
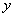предполагает, что медианный центр, обозначенный звездочкой, будет находиться в области точек 1, 2 и 4, так как выше и ниже его должны находиться по две точки. Таким образом, выброс в точке 3 на сглаженной зависимости будет устранен.
Необходимо иметь в виду, что зависимост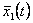и и 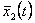, полученные методом скользящего среднего и методом медианного сглаживания отличаются. Их отличие возрастает при увеличении частоты возникновения аномальных выбросов. Если выбросы возникают в анализируемой временной зависимости достаточно часто, то они могут рассматриваться как неотъемлемая характеристика флуктуационной составляющей и их устранение при сглаживании искажает адекватное описание случайного ряда. Для оценки частоты выбросов могут использоваться разные критерии, например, средняя частота возникновения выбросов на выбранном временном интервале или отношение их общего количества к длине временного ряда.
Фильтрация – уменьшение шумовой составляющей из полезного измерительного сигнала.
Сначала анализируют причины возникновения шумов и пытаются их устранить.
Если сигнал периодический, используют синхронную фильтрацию.
Рис., формулы
