Ссылка на Сато.
Экстраполяция, интерполяция, аппроксимация.
Статистические модели, которые позволяют оценить неоднозначность образа действительности называются мерами.
Эти меры позволяют оценить неоднозначность в узком смысле, по сравнению с Pa(b) – дифференциальной (интегрально) функцией распределения вероятности.
Группы мер:
1. Меры позволяющие оценить отклонения характеристик от значения b*, которое наиболее достоверно описывает образ действительности:
а) Средневзвешенное отклонение
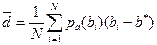 ;
;
б) Среднеквадратичное, или стандартное отклонение (средневзвешенное) ошибка
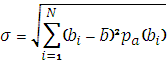 для дискретных результатов
для дискретных результатов
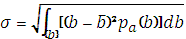 для непрерывных результатов
для непрерывных результатов
в) Центральные моменты (средневзвешенные)
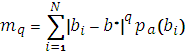
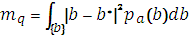
2. Меры близкие к мерам Лебега.
М.Л. – мера, позволяющая представить множество значений в геометрической форме.
Эти меры находят при выделении частного подмножества из множества результатов измерений за счёт предъявления жёсткого условия:
- 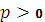
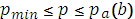
При этом выделенное подмножество:
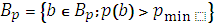
Множество 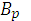 характеризуется мерой Лебега.
характеризуется мерой Лебега.
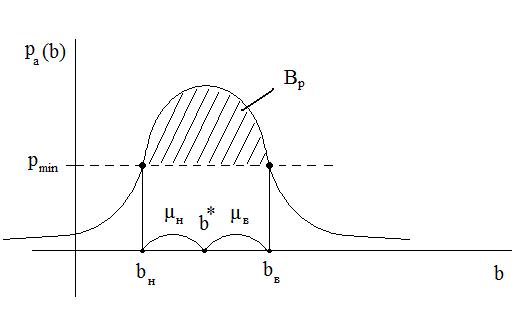
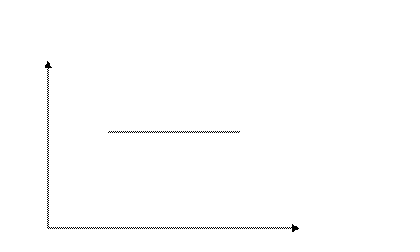
Рис. 2.3.1. Графическая интерпретация интервальной меры
Мера Лебега:
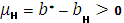
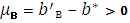
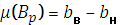
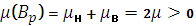
В данном случае мерой Лебега становится доверительный интервал, ширина которого определяется pmin – минимальным значением вероятности:
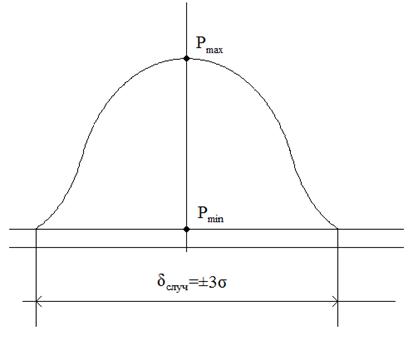
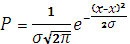
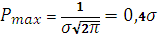
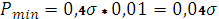
Этой мерой можно оценивать только мономодальные, или унимодальные распределения.
3. Мера близкие к мере Лебега, позволяющая выделить подмножества Bα с учётом следующего условия:
это подмножество должно содержать какую-то заданную часть элементов общего множества.
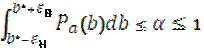
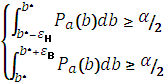
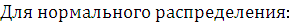
ошибка
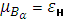
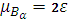 - доверительный интервал
- доверительный интервал
Мера Лебега по сути является доверительным интервалом:
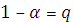
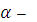 доверительная вероятность
доверительная вероятность
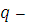 уровень значимости (допустимая ошибка!!!!)
уровень значимости (допустимая ошибка!!!!)
4. Энтропия
Мера неупорядоченности:
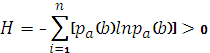
Логарифмическая мера определенного интервала, длина которого зависит от распределения вероятности:
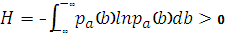
Наибольшую энтропию (степень неопределенности) имеют результаты измерения, описываемые равновероятностным законом распределения:
Для множества с равномерным распределением вероятности:
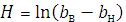
Для множества с нормальным распределением вероятности:
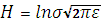
 2014-02-24
2014-02-24 620
620








