Достоинства множества Парето
Подводя итог рассмотрению множества Парето, можно отметить его следующие достоинства:
1. Множество Парето можно строить не только для количественных критериев, но и для качественных.
2. Построение множества Парето позволяет существенно (в десятки и сотни раз) сократить количество рассматриваемых альтернатив и тем самым сократить время их анализа при определении лучшей альтернативы с помощью сильного обобщённого критерия.
3. Построение множества Парето не требует назначения весовых коэффициентов.
4. Множество Парето позволяет избавиться от необходимости назначения весовых коэффициентов.
Достаточно часто у ЛПР возникает вопрос, каким сильным критерием лучше пользоваться: аддитивным или мультипликативным? К сожалению, однозначного ответа дать нельзя. Дело в том, что каждый из этих критериев соответствует определённому мироощущению ЛПР: равнодушному отношению к действительности или пессимистическому. Чтобы показать связь указанных критериев с мироощущением ЛПР, рассмотрим так называемое поле выбора решений. Пусть заданы ограничения на критерии a1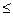 y1
y1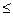 a2, b1
a2, b1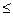 y2
y2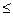 b2. Поле выбора решения — это область, определяемая ограничениями на y1 и y2.
b2. Поле выбора решения — это область, определяемая ограничениями на y1 и y2.
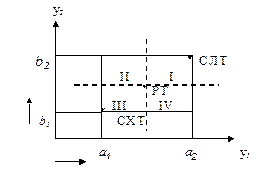
В поле выбора решения можно указать следующие характерные точки:
СЛТ — самая лучшая точка (утопическая точка); она обычно недостижима, так как y1 и y2 одновременно не могут принять своих наилуших значений.
СХТ — самая худшая точка; (антиутопическая точка);
РТ — рассматриваемая точка.
Рассмотрим квадранты поля выбора I, II, III и IV. Все точки в квадранте I лучше РТ, так как в них y1 и y2 больше, чем в РТ, независимо от точки зрения ЛПР. Все точки в квадранте III хуже РТ, так как в них y1 и y2 меньше, чем в РТ, независимо от точки зрения ЛПР. В квадрантах II, IV качество точек (лучше, хуже чем в РТ) не определенно и зависит от точки зрения ЛПР.
Рассмотрим сначала аддитивный критерий. Пусть ЛПР одинаково относится к критериям y1 и y2. Тогда линия уровня Y=0.5*y1+0.5*y2=const — это линия равнодушия или нейтральная в смысле предпочтения ЛПР. После нормировке критериев поле выбора решения станет квадратом, а нейтральная линия уровня — бисcектрисой областей II и IV. Эта биссектриса делит квадранты II и IV на равные треугольные части, где один треугольник содержит точки, лучшие, чем на биссектрисе, а второй – худшие. Точки областей II и IV над нейтральной линией — лучше, чем на этой линии, а под ней — хуже. Их количество одинаковое. Можно интерпретировать этот факт как равнодушное мироощущуение ЛПР – в окружающем мире хорошего и плохого поровну.
Рассмотрим теперь мультипликативный критерий. Как известно, линией уровня для него служит гипербола, которая делит квадранты II и IV на неравные части, где часть с точками хуже чем на гиперболе больше части с точками лучше чем на гиперболе. Таким образом, использование ЛПР мультипликативного критерия означает, что ЛПР пессимистически смотрит на окружающий мир, в котором плохого больше, чем хорошего.
По аналогичным причинам оптимистический критерий должен иметь линии уровня с обратной по сравнению с мультипликативным критерием кривизной. Таким образом, выбор ЛПР аддитивного или мультипликативного критерия должен соответствовать его мироощущению, а вопрос, какой критерий лучше, просто некорректен.
Второй весьма популярный вопрос, возникающий у ЛПР, заключается в следующем. Если какая-то альтернатива оказалась лучшей по одному обобщённому критерию, например аддитивному, то должна ли она быть лучше и по другим обобщённым критериям, например, мультипликативному? Ответ: одна и та же альтернатива может быть лучше другой по одному критерию, но хуже по другому. В качестве иллюстрации рассмотрим таблицу принятия решений
| Частные критерии Альтернативы | у1 | у2 |
| A1 | ||
| А2 |
Для простоты будем считать частные критерии у1 и у2 «хорошими», имеющими одинаковую размерность (нормирование не требуется) и равноценными (весовые коэффициенты равны единице). Тогда аддитивный критерий даст значения Y1=2+3=5; Y2=5+1=6, то есть альтернатива А2 лучше А1. Мультипликативный же критерий даст Y1=2x3=6; Y2=5x1=5, то есть альтернатива А1 лучше А2. Приведенный пример говорит о том, что сумма и произведение одних и тех же чисел могут находиться в разных отношениях друг к другу.
 2014-02-24
2014-02-24 856
856








